Home /
Expert Answers /
Advanced Math /
on-a-day-when-the-sun-passes-directly-overhead-at-noon-a-6-ft-tall-man-casts-a-shadow-of-length-6-s-pa623
(Solved): On a day when the sun passes directly overhead at noon, a 6-ft-tall man casts a shadow of length 6 s ...
On a day when the sun passes directly overhead at noon, a 6-ft-tall man casts a shadow of length 6 s(t) = tan 12 where S is measured in feet and it is the number of hours since 6 A.M. 7:00 A.M. S (a) Find the length of the shadow at 7:00 A.M., noon, and 2:00 P.M. (Round your answers to two decimal places.) ft 0 S 51 6 ft noon ft 2:00 P.M. (b) Sketch a graph of the function S for 0 < t < 12. ft S
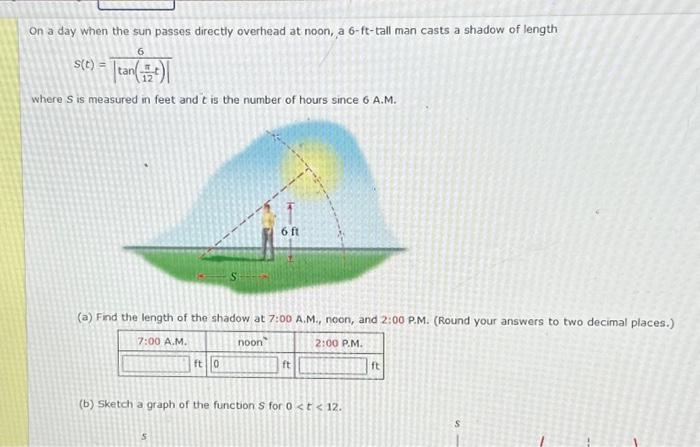
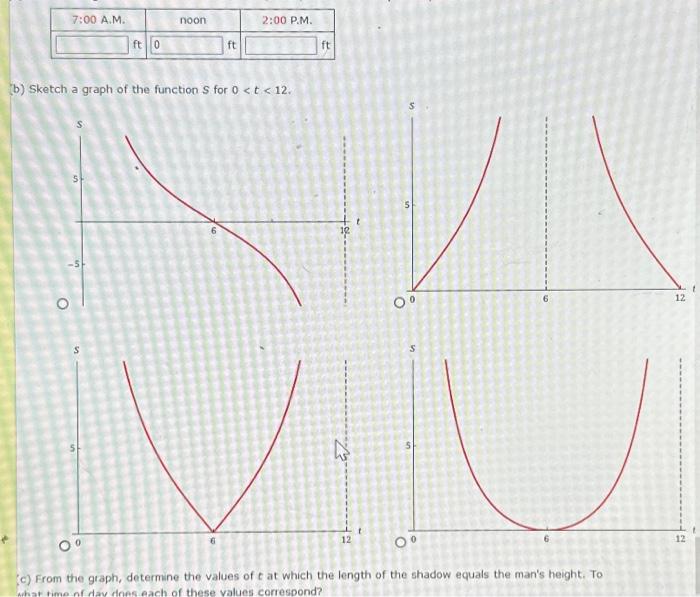

On a day when the sun passes directly overhead at noon, a 6- -tall man casts a shadow of length where is measured in feet and is the number of hours since 6 A.M. (a) Find the length of the shadow at 7:00 A.M., noon, and 2:00 P.M. (Round your answers to (b) Sketch a graph of the function for .
b) Sketch a graph of the function for . (c) From the graph, determine the values of at which the length of the shadow equals the man's height. To
(c) From the graph, determine the values of at which the length of the shadow equals the man's height. To what time of day does each of these values correspond? ; that is, at noon and ; that is, at 11:00 A.M. and 1:00 P.M and that is, at 7:00 A.M. and 5:00 P.M and that is, at 3:00 A.M. and 9:00 P.M and that is, at 9:00 A.M. and 3:00 P.M (d) Explain what happens to the shadow as the time approaches 6 P.M. (that is, as ). The shadow gets increasingly longer. The length of the shadow approaches 6 feet. The length of the shadow approaches 12 feet. The length of the shadow approaches 46 feet. The shadow gets increasingly shorter.
Expert Answer
To find the length of the shadow at 7:00 A.M., noon, and 2:00 P.M., we can substitute the respective...