Home /
Expert Answers /
Calculus /
nbsp-use-a-double-integral-to-find-the-area-of-the-region-defined-as-one-loop-of-the-rose-r-pa701
(Solved): Use a double integral to find the area of the region defined as one loop of the rose \( r= ...
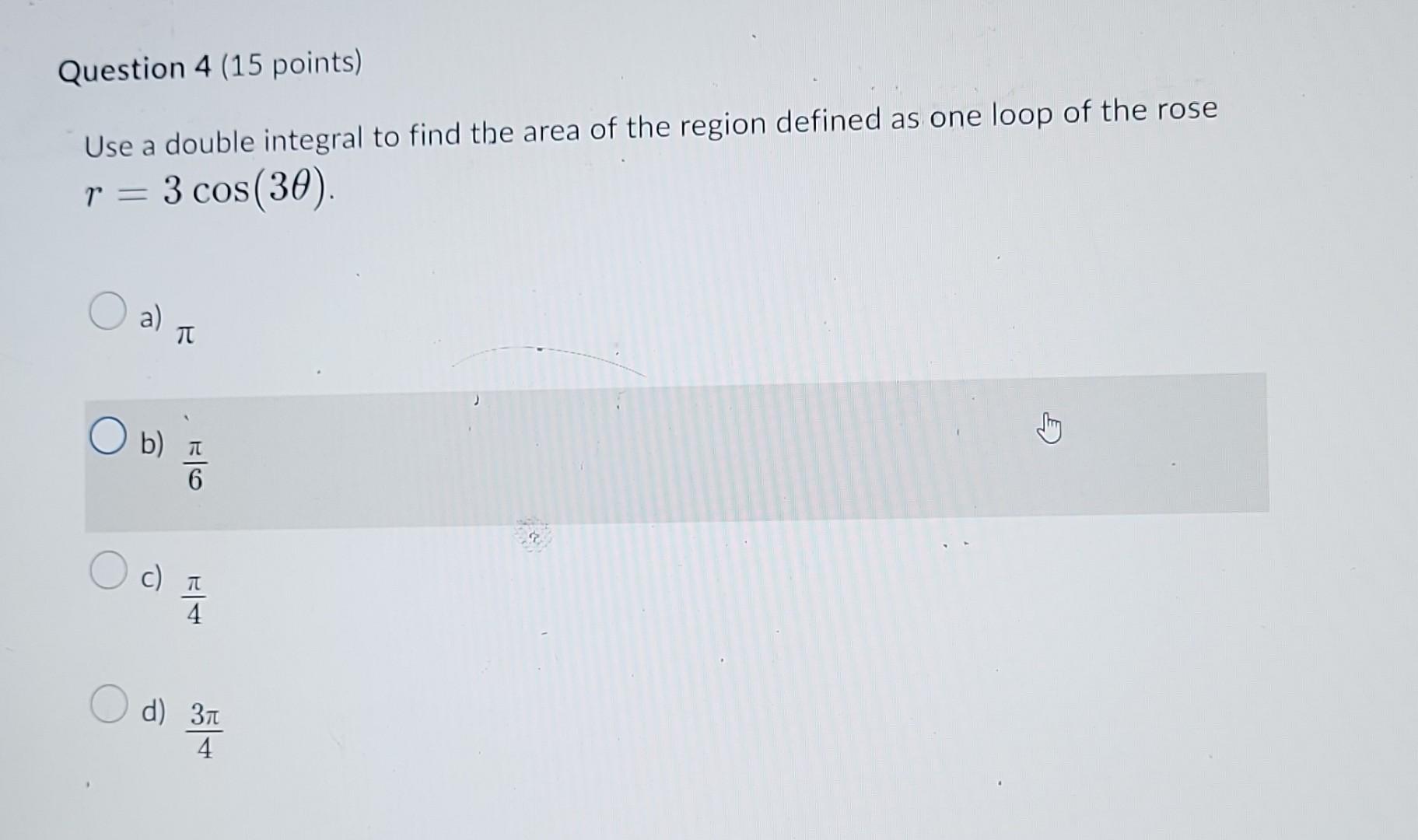
Use a double integral to find the area of the region defined as one loop of the rose \( r=3 \cos (3 \theta) \). a) \( \pi \) b) \( \frac{\pi}{6} \) c) \( \frac{\pi}{4} \) d) \( \frac{3 \pi}{4} \)
Expert Answer
We have to find the area of region defined as one loop of the rose by using double integral: r=3cos?(3?) Finding point of intersections, r=03cos?(3?)=