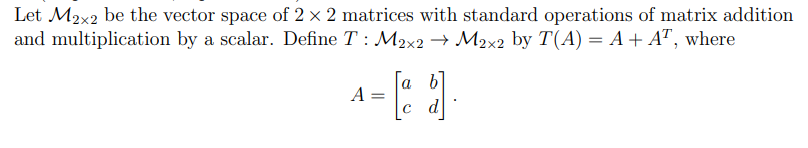(Solved):   help linear algerba ! Let \( \mathcal{M}_{2 \times 2} \) be the vector space of \( 2 \tim ...

 

help linear algerba !

Let \( \mathcal{M}_{2 \times 2} \) be the vector space of \( 2 \times 2 \) matrices with standard operations of matrix addition and multiplication by a scalar. Define \( T: \mathcal{M}_{2 \times 2} \rightarrow \mathcal{M}_{2 \times 2} \) by \( T(A)=A+A^{T} \), where \[ A=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right] \] (a) Show that \( T \) is a linear transformation; (b) Let \( B \in \mathcal{M}_{2 \times 2} \) be such that \( B=B^{T} \). Find \( A \in \mathcal{M}_{2 \times 2} \) such that \( T(A)=B \); (c) Show that \( R(T)=\left\{B \in \mathcal{M}_{2 \times 2} \mid B=B^{T}\right\} \); (d) Describe \( \operatorname{Ker}(T) \).