(Solved):   A port and a radar station are \( 4 \mathrm{mi} \) apart on a straight shore running eas ...

 

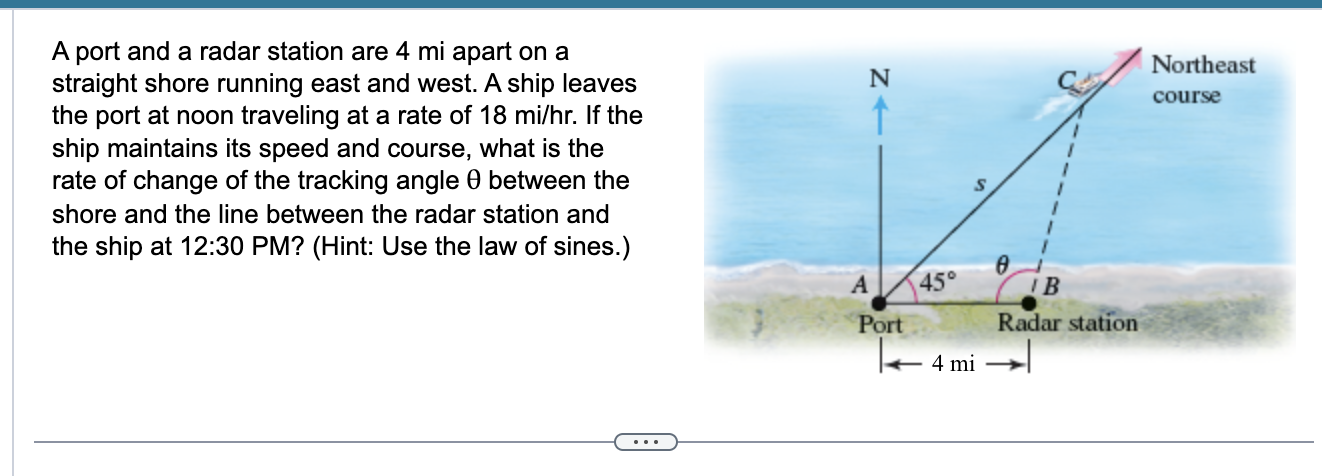
A port and a radar station are \( 4 \mathrm{mi} \) apart on a straight shore running east and west. A ship leaves the port at noon traveling at a rate of \( 18 \mathrm{mi} / \mathrm{hr} \). If the ship maintains its speed and course, what is the rate of change of the tracking angle \( \theta \) between the shore and the line between the radar station and the ship at 12:30 PM? (Hint: Use the law of sines.) Use the Law of Sines to find an equation relating the angle, \( \theta \), the angle that the ship left the port at, the distance between the radar system and the ship, a, and the distance between the port and the ship, s. Evaluate any known trigonometric functions of \( 45^{\circ} \) as needed. (Type an exact answer.) Find the related rates equation, evaluating any trigonometric functions of \( \left(45^{\circ}\right) \) as needed. \[ \frac{d \theta}{d t}=\left(\left\{\begin{array}{l} c \end{array}\right)\left(a \frac{d s}{d t}-s \frac{d a}{d t}\right)\right. \] The rate of change of the tracking angle 0 between the shore and the line between the radar station and the ship at \( 12: 30 \) PM is (Round to four decimal places as needed.)