(Solved):   2. A juggler is juggling a uniform rod, one end of which is coated in tar and burning. He ...

 

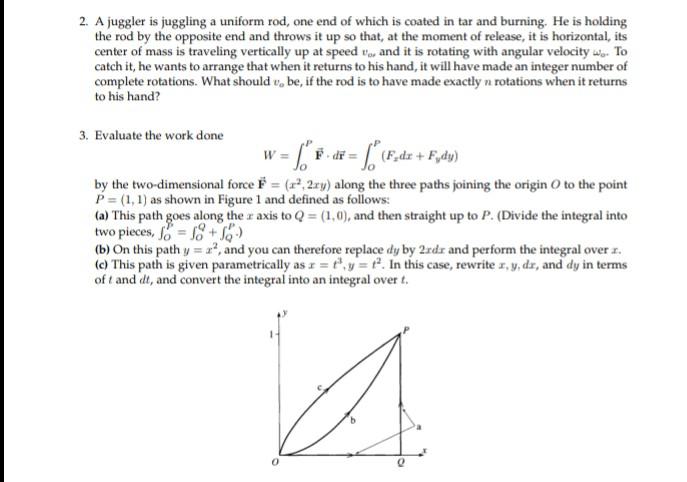
2. A juggler is juggling a uniform rod, one end of which is coated in tar and burning. He is holding the rod by the opposite end and throws it up so that, at the moment of release, it is horizontal, its center of mass is traveling vertically up at speed \( v_{a,} \) and it is rotating with angular velocity \( \omega_{o} \). To catch it, he wants to arrange that when it returns to his hand, it will have made an integer number of complete rotations. What should \( v_{\mathrm{o}} \) be, if the rod is to have made exactly \( n \) rotations when it returns to his hand? 3. Evaluate the work done \[ W=\int_{O}^{P} \overrightarrow{\mathbf{F}} \cdot d \overrightarrow{\mathbf{r}}=\int_{O}^{P}\left(F_{x} d x+F_{y} d y\right) \] by the two-dimensional force \( \overrightarrow{\mathbf{F}}=\left(x^{2}, 2 x y\right) \) along the three paths joining the origin \( O \) to the point \( P=(1,1) \) as shown in Figure 1 and defined as follows: (a) This path goes along the \( x \) axis to \( Q=(1,0) \), and then straight up to \( P \). (Divide the integral into two pieces, \( \int_{O}^{8}=\int_{O}^{Q}+\int_{Q}^{P} \) ) (b) On this path \( y=x^{2} \), and you can therefore replace \( d y \) by \( 2 x d x \) and perform the integral over \( x \). (c) This path is given parametrically as \( x=t^{3}, y=t^{2} \). In this case, rewrite \( x, y, d x \), and \( d y \) in terms of \( t \) and \( d t \), and convert the integral into an integral over \( t \).