(Solved):   10. Prove that union of any finite number of countably infinite sets is countably infinite ...

 

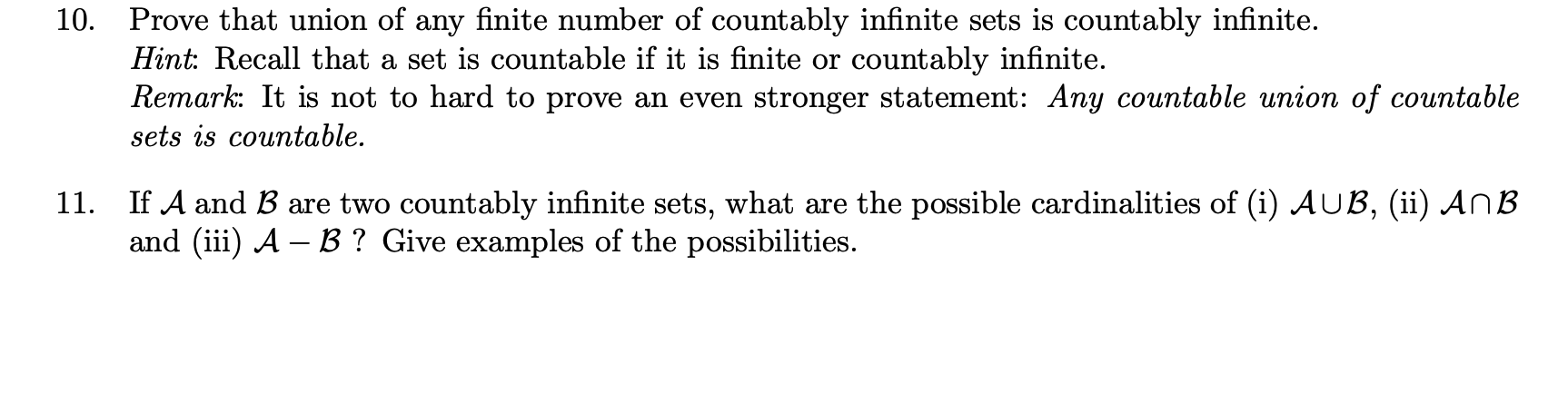
10. Prove that union of any finite number of countably infinite sets is countably infinite. Hint: Recall that a set is countable if it is finite or countably infinite. Remark: It is not to hard to prove an even stronger statement: Any countable union of countable sets is countable. 11. If \( \mathcal{A} \) and \( \mathcal{B} \) are two countably infinite sets, what are the possible cardinalities of (i) \( \mathcal{A} \cup \mathcal{B} \), (ii) \( \mathcal{A} \cap \mathcal{B} \) and (iii) \( \mathcal{A}-\mathcal{B} \) ? Give examples of the possibilities.