(Solved):   1. Analysis and design of a buck-boost converter. A buck-boost converter is illustrat ...

 

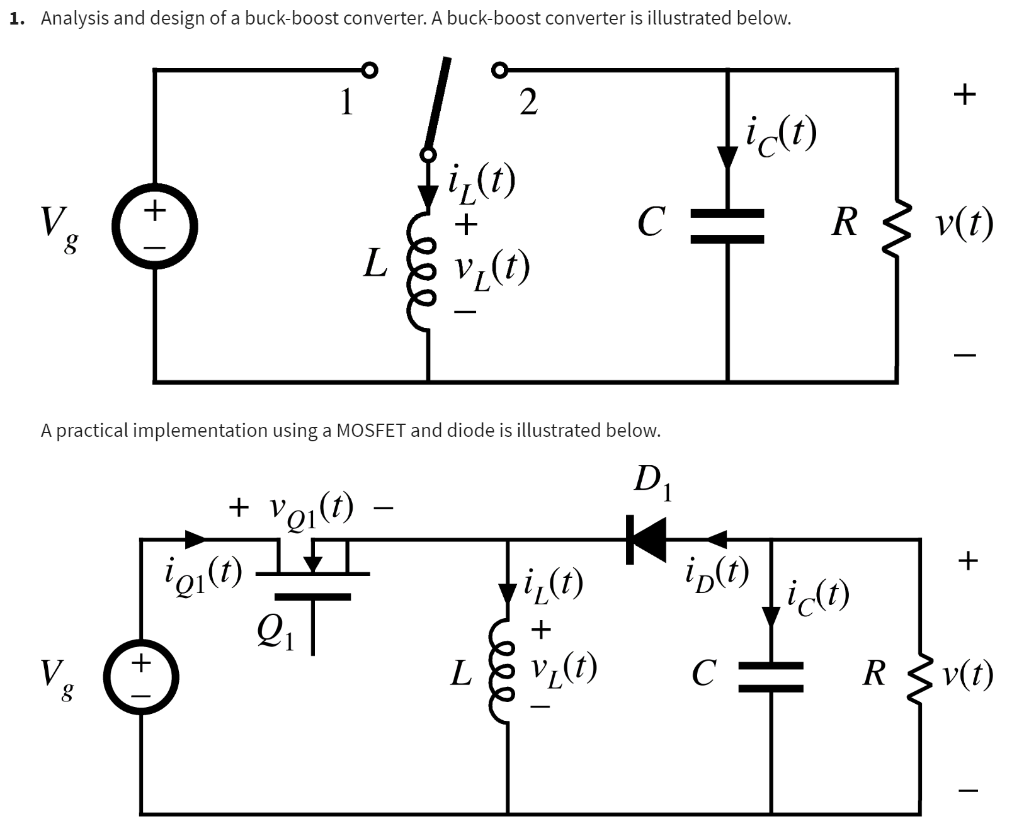
1. Analysis and design of a buck-boost converter. A buck-boost converter is illustrated below. A practical implementation using a MOSFET and diode is illustrated below. For this problem, you must employ the methods of inductor volt-second balance, capacitor charge balance, and the small ripple approximation as discussed in the lectures, to analyze this converter and find analytical expressions for the output voltage, inductor current, etc. You are asked to enter expressions for intermediate steps in your analysis; these expressions must be entered as computer-readable equations using the exact variable names and reference polarities defined in the figures above. The dc components of the relevant signals, as well as other quantities, are defined below: - Input voltage Vg - Output voltage V - Duty cycle D - Switching period Ts - Load resistance R - Inductance L - Capacitance C - Inductor current IL - Inductor voltage VL - Transistor voltage VQ1 - Transistor current IQ1 - Diode current ID When entering equations, these variable names are case-sensitive and must be entered exactly as defined above; for example, \( D^{*}(\mathrm{Vg}-\mathrm{V}) / \mathrm{R} \). The complement of the duty cycle should be entered as (1-D). When numeric values are requested, a single numeric value must be entered that is accurate to within plus or minus \( 0.1 \% \) of the value computed using the methods described in lecture. To work this homework assignment, it is highly recommended that you first sketch the converter circuit and work the questions with pencil and paper. Then enter your answers into the fields below. The questions sometimes ask you to sketch waveforms; this is intended for guidance only, and you are not asked to actually upload or enter a waveform. Sketch the waveform of the inductor voltage \( v_{L}(t) \). Employ the small ripple approximation to derive an expression for the dc component of the inductor voltage, as a function of the duty cycle \( \mathrm{D} \) and the \( \mathrm{dc} \) capacitor voltage \( \mathrm{V} \) and source voltage Vg. Enter your expression below. \( D V g+V(-D+1) \) Please note: Each of the following will be interpreted as a single variable, not as a product of variables: Vg. To multiply variables, please use * \( \left(\right. \) e.g. enter \( x^{*} y \) to multiply variables \( x \) and \( y \) ). Sketch the waveform of the capacitor current \( i_{C}(t) \). Employ the small ripple approximation to derive an expression for the dc component of the capacitor current, as a function of the duty cycle \( \mathrm{D} \), the dc inductor current IL, the output voltage V, and the load resistance R. Enter your expression below. \[ \frac{D V}{R}+(-D+1)\left(-I L+\frac{V}{R}\right) \] Please note: Each of the following will be interpreted as a single variable, not as a product of variables: IL. To multiply variables, please use * (e.g. enter \( x^{*} y \) to multiply variables \( x \) and \( y \) ). 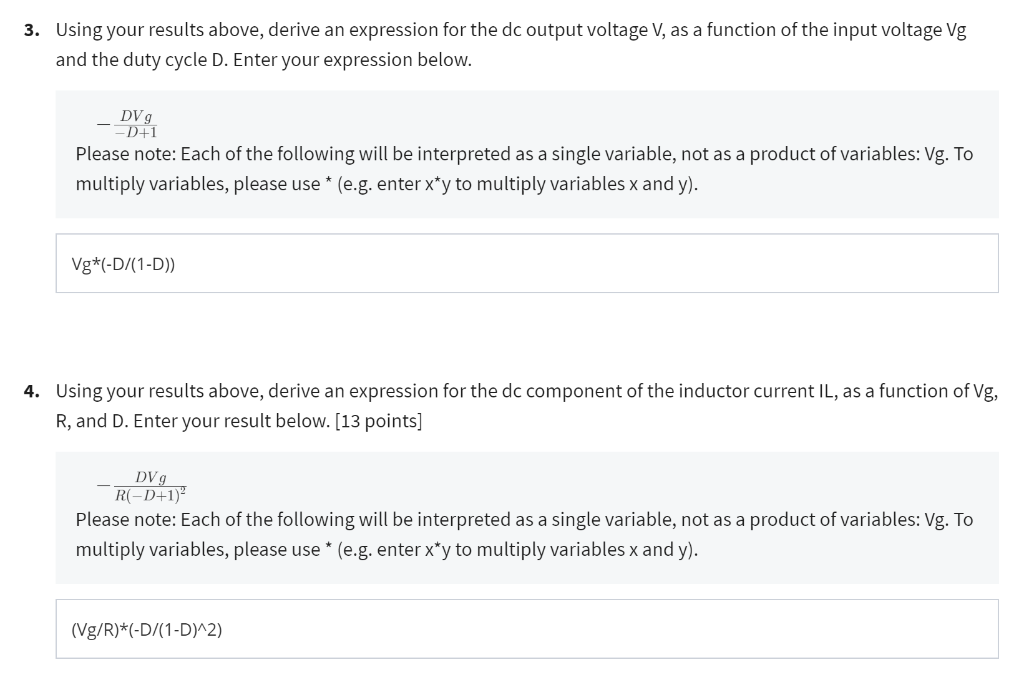Using your results above, derive an expression for the dc output voltage V, as a function of the input voltage Vg and the duty cycle D. Enter your expression below. \( -\frac{D V g}{-D+1} \) Please note: Each of the following will be interpreted as a single variable, not as a product of variables: \( \mathrm{Vg} \). To multiply variables, please use * \( \left(\right. \) e.g. enter \( x^{*} y \) to multiply variables \( x \) and \( y \) ). Using your results above, derive an expression for the dc component of the inductor current IL, as a function of Vg R, and D. Enter your result below. [13 points] \( -\frac{D V g}{R(-D+1)^{2}} \) Please note: Each of the following will be interpreted as a single variable, not as a product of variables: \( V \). To multiply variables, please use * \( \left(\right. \) e.g. enter \( x^{*} y \) to multiply variables \( x \) and \( y \) ). Derive an expression for the inductor peak current ripple (denoted "delta \( i \) " in the lectures). Express your result in terms of \( \mathrm{Vg}, \mathrm{D}, \mathrm{Ts} \), and \( \mathrm{L} \), and enter the result below. \( \frac{D T s V g}{2 L} \) Please note: Each of the following will be interpreted as a single variable, not as a product of variables: \( V \), To multiply variables, please use \( ^{*}\left(\right. \) e.g. enter \( x^{\star} y \) to multiply variables \( x \) and \( y \) ). Derive an expression for the capacitor peak voltage ripple (denoted "delta \( v^{\prime} \) in the lectures). Express your result in terms of Vg, D, Ts, C, and R, and enter the result below. Assume that the capacitor is ideal and lossless. \[ \frac{D^{2} T s V g}{2 C R(D-1)} \] Please note: Each of the following will be interpreted as a single variable, not as a product of variables: Vg, Ts. To multiply variables, please use * \( \left(\right. \) e.g. enter \( x^{*} y \) to multiply variables \( x \) and \( y \) ). For questions \( 7-13 \), it is desired to design a buck-boost converter that meets the following specifications: - Input voltage \( \mathrm{Vg}=12 \mathrm{~V} \) - Output voltage V \( =-5 \mathrm{~V} \) - \( \quad \) Load resistance \( \mathrm{R}=2.5 \mathrm{Ohms} \) - Switching frequency \( \mathrm{fs}=1 / \mathrm{Ts}=200 \mathrm{kHz} \) All elements are ideal. Compute the numerical value of the duty cycle D, and enter its value below. Again, enter this and other numerical values with an accuracy of at least plus or minus \( 0.1 \% \). Compute the numerical value of the dc component of the inductor current, in amperes. Enter your value below. Calculate the value of the inductance \( L \) that will make the peak inductor current ripple ("delta i") equal to fifteen percent of the dc component of inductor current. Express your result in micro henries, and enter the numerical value below. 0. Compute the value of capacitance \( \mathrm{C} \) that will cause the output voltage peak ripple ("delta v") to be equal to 25 mV. Express your result in micro farads, and enter the numerical value below. 1. For the design with numerical values as specified above, sketch the waveform of the MOSFET current waveform \( i_{Q_{1}}(t) \), including ripple. Find its peak value in amperes, and enter the numerical value below. 2. For the design with numerical values as specified above, sketch the waveform of the MOSFET voltage \( v_{Q 1}(t) \), including ripple. Find its peak value in volts, and enter the numerical value below. 3. For your MOSFET voltage waveform \( v_{Q_{1}}(t) \) of the previous question: compute the dc component of this waveform, and enter its numerical value below.