(Solved): \( \mu \) also called A. Standard Error. Se also called B. \( 1-p^{\wedge} \) p-value-also called p ...

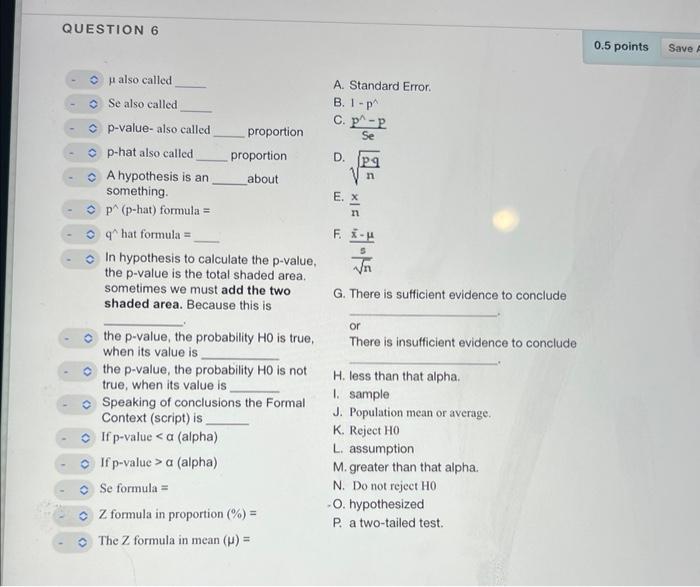
\( \mu \) also called A. Standard Error. Se also called B. \( 1-p^{\wedge} \) p-value-also called proportion C. \( \frac{\mathrm{p}^{\wedge}-\mathrm{p}}{\mathrm{Se}} \) p-hat also called proportion A hypothesis is an about D. \( \sqrt{\frac{p q}{n}} \) something. \( p^{\wedge} \) (p-hat) formula \( = \) E. \( \frac{x}{n} \) \( \mathrm{q}^{\wedge} \) hat formula \( = \) sometimes we must add the two shaded area. Because this is G. There is sufficient evidence to conclude the p-value, the probability \( \mathrm{HO} \) is true, There is insufficient evidence to conclude when its value is the p-value, the probability \( \mathrm{HO} \) is not true, when its value is \( H \). less than that alpha. Speaking of conclusions the Formal I. sample Context (script) is J. Population mean or average. If \( \mathrm{p} \)-value \( <\alpha \) (alpha) K. Reject \( \mathrm{HO} \) If p-value \( >\alpha \) (alpha) L. assumption Se formula \( = \) M. greater than that alpha. N. Do not reject H0 \( Z \) formula in proportion \( (\%)= \) -O. hypothesized The \( Z \) formula in mean \( (\mu)= \) P. a two-tailed test.