(Solved): Most analytical machines used in science can either measure absorbance of light, like the spectrop ...

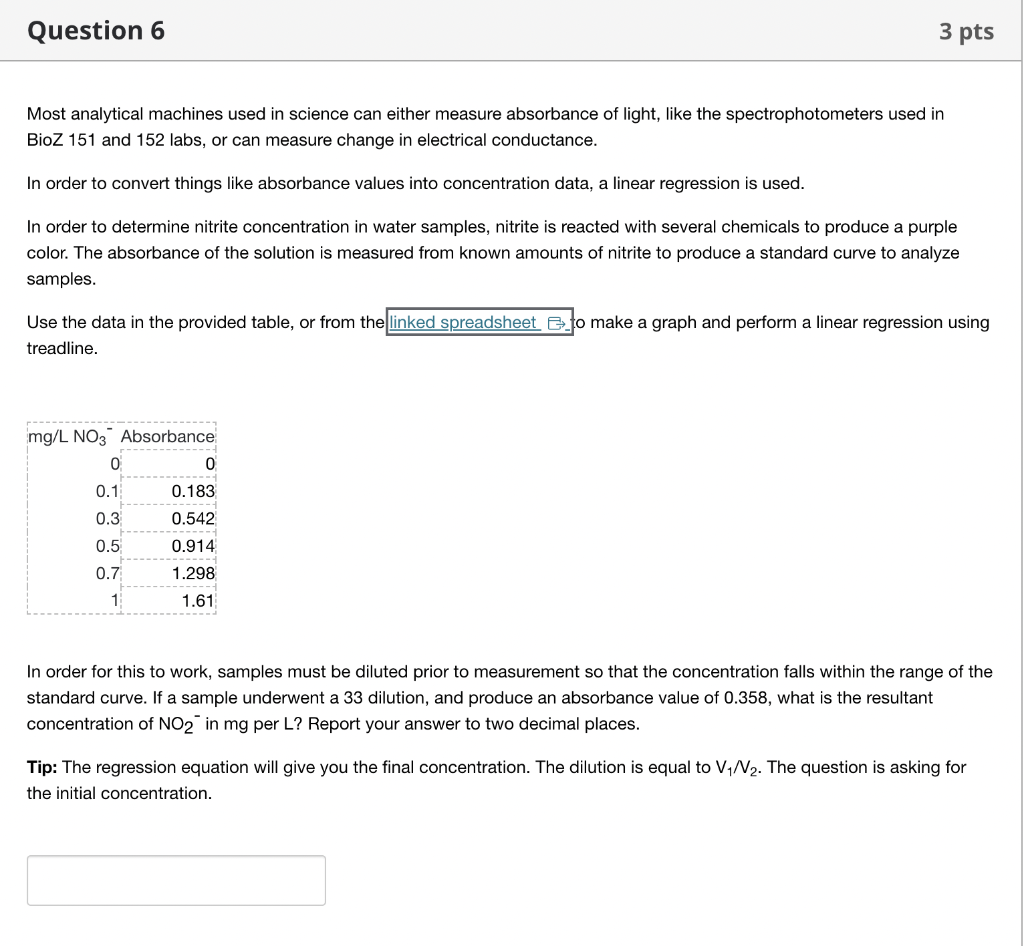
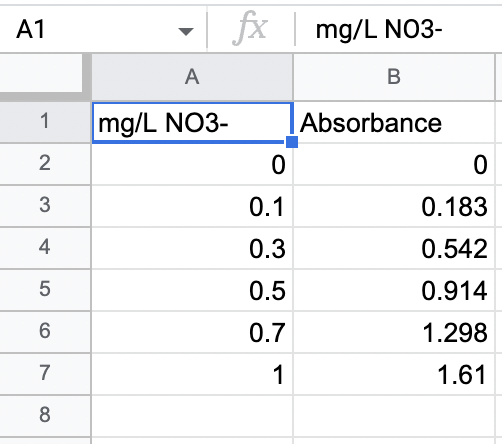
Most analytical machines used in science can either measure absorbance of light, like the spectrophotometers used in BioZ 151 and 152 labs, or can measure change in electrical conductance. In order to convert things like absorbance values into concentration data, a linear regression is used. In order to determine nitrite concentration in water samples, nitrite is reacted with several chemicals to produce a purple color. The absorbance of the solution is measured from known amounts of nitrite to produce a standard curve to analyze samples. Use the data in the provided table, or from the o make a graph and perform a linear regression using treadline. In order for this to work, samples must be diluted prior to measurement so that the concentration falls within the range of the standard curve. If a sample underwent a 33 dilution, and produce an absorbance value of \( 0.358 \), what is the resultant concentration of \( \mathrm{NO}_{2}^{-} \)in mg per L? Report your answer to two decimal places. Tip: The regression equation will give you the final concentration. The dilution is equal to \( V_{1} / N_{2} \). The question is asking for the initial concentration. \begin{tabular}{|r|r|r|} \hline A1 & \( f X \) & \multicolumn{2}{|c|}{\( \mathrm{mg} / \mathrm{L} \mathrm{NO3-} \)} \\ \hline \multicolumn{1}{|c|}{\( \mathrm{A} \)} & \multicolumn{1}{c|}{\( \mathrm{B} \)} \\ \hline 1 & \( \mathrm{mg} / \mathrm{L} \mathrm{NO3-} \) & Absorbance \\ \hline 2 & 0 & 0 \\ \hline 3 & \( 0.1 \) & \( 0.183 \) \\ \hline 4 & \( 0.3 \) & \( 0.542 \) \\ \hline 5 & \( 0.5 \) & \( 0.914 \) \\ \hline 6 & \( 0.7 \) & \( 1.298 \) \\ \hline 7 & 1 & \( 1.61 \) \\ \hline 8 & & \\ \hline \end{tabular}