(Solved): Matrix \( \mathrm{A} \) is factored in the form \( \mathrm{PDP}^{-1} \). Use the Diagonalization T ...

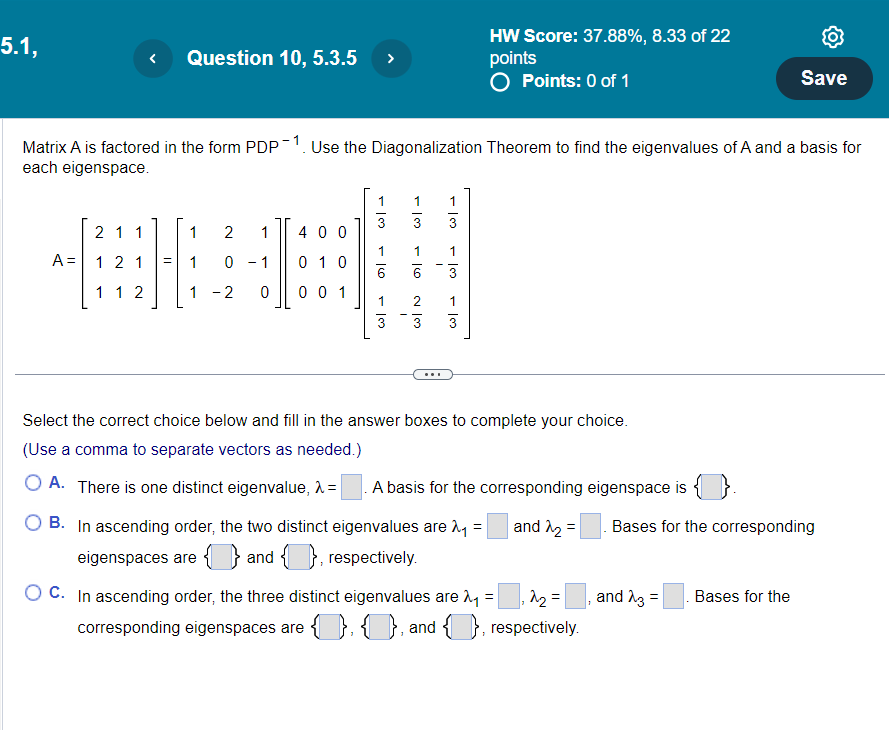
Matrix \( \mathrm{A} \) is factored in the form \( \mathrm{PDP}^{-1} \). Use the Diagonalization Theorem to find the eigenvalues of \( \mathrm{A} \) and a basis for each eigenspace. \[ A=\left[\begin{array}{lll} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \end{array}\right]=\left[\begin{array}{rrr} 1 & 2 & 1 \\ 1 & 0 & -1 \\ 1 & -2 & 0 \end{array}\right]\left[\begin{array}{lll} 4 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{rrr} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{6} & \frac{1}{6} & -\frac{1}{3} \\ \frac{1}{3} & -\frac{2}{3} & \frac{1}{3} \end{array}\right] \] Select the correct choice below and fill in the answer boxes to complete your choice. (Use a comma to separate vectors as needed.) A. There is one distinct eigenvalue, \( \lambda= \) A basis for the corresponding eigenspace is . B. In ascending order, the two distinct eigenvalues are \( \lambda_{1}= \) and \( \lambda_{2}= \). Bases for the corresponding eigenspaces are.' and ', respectively. C. In ascending order, the three distinct eigenvalues are \( \lambda_{1}=, \lambda_{2}= \), and \( \lambda_{3}= \) Bases for the corresponding eigenspaces are , , , and, , respectively.