(Solved): Learning Goal: To calculate the shear stress at the web/flange joint in a beam and use that stress ...

Learning Goal: To calculate the shear stress at the web/flange joint in a beam and use that stress to calculate the required nail spacing to make a built-up beam. A built up beam can be constructed by fastening flat plates together. When an I-beam is subjected to a shear load, internal shear stress is developed at every cross section, with longitudinal shear stress balancing transverse shear stress. If the beam is built up using plates, the fasteners used must be able to resist the shear at the joints. The loading resisted by the fasteners can be described in the force per unit length of the beam and is called the shear flow. The shear flow at some distance $y$ from the neutral axis can be calculated using the shear formula $q=\frac{VQ}{I}$, where $V$ is the shear force, $Q$ is the moment about the centroidal axis of the cross-sectional area above $y$, and $I$ is the moment of inertia of the cross section. Since the nals are joining the flanges to the web, they must resist the shear flow at the joint What is the maximum spacing for the nals if each nail can support a shear force of $240\mathrm{lb}$ ? Express your answer with appropriate units to three significant figures. 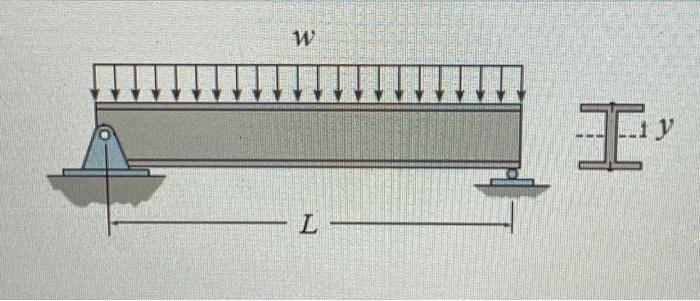An engineered wood beam (Eigure 1) will replace a portion of a structural wall as part of a house renovation. The beam can be modeled as a simply supported beam with a span $L=17\mathrm{ft}$ and an uniform distributed load $w=855\mathrm{lb}/\mathrm{ft}$. The beam is to be constructed as an 1 -beam with nails securing the flanges to the web. The flanges are 6 in wide and 1 in thick. The web has depth 18 in and thickness 3 in. The maximum allowable shear stress in the web is 900 psi Part A - Maximum shear load Assuming the joints do not fail, what is the maximum shear load the beam can support? Express your answer with appropriate units to three significant figures. Part B - Shear flow at joint What is the maximum shear flow at the joints connecting the web and flange under the applied load of $w=855\mathrm{lb}/\mathrm{ft}$ ? Express your answer with appropriate units to three significant figures. Learning Goal: To calculate the shear stress at the web/flange joint in a beam and use that stress to calculate the required nail spacing to make a built-up beam. A built up beam can be constructed by fastening flat plates together. When an I-beam is subjected to a shear load, internal shear stress is developed at every cross section, with longitudinal shear stress balancing transverse shear stress. If the beam is built up using plates, the fasteners used must be able to resist the shear at the joints. The loading resisted by the fasteners can be described in the force per unit length of the beam and is called the shear flow. The shear flow at some distance $y$ from the neutral axis can be calculated using the shear formula $q=\frac{VQ}{I}$, where $V$ is the shear force, $Q$ is the moment about the centroidal axis of the cross-sectional area above $y$, and $I$ is the moment of inertia of the cross section. Since the nals are joining the flanges to the web, they must resist the shear flow at the joint What is the maximum spacing for the nals if each nail can support a shear force of $240\mathrm{lb}$ ? Express your answer with appropriate units to three significant figures. An engineered wood beam (Eigure 1) will replace a portion of a structural wall as part of a house renovation. The beam can be modeled as a simply supported beam with a span $L=17\mathrm{ft}$ and an uniform distributed load $w=855\mathrm{lb}/\mathrm{ft}$. The beam is to be constructed as an 1 -beam with nails securing the flanges to the web. The flanges are 6 in wide and 1 in thick. The web has depth 18 in and thickness 3 in. The maximum allowable shear stress in the web is 900 psi Part A - Maximum shear load Assuming the joints do not fail, what is the maximum shear load the beam can support? Express your answer with appropriate units to three significant figures. Part B - Shear flow at joint What is the maximum shear flow at the joints connecting the web and flange under the applied load of $w=855\mathrm{lb}/\mathrm{ft}$ ? Express your answer with appropriate units to three significant figures.