Home /
Expert Answers /
Mechanical Engineering /
j-o-b-ar-j-c-39-ad-2-where-i-x-is-the-area-39-s-moment-of-inertia-about-the-noncentroida-pa333
(Solved): J_(O)()/(b)=ar (J)_(C^('))+Ad^(2) where I_(x) is the area's moment of inertia about the noncentroida ...
J_(O)()/(b)=ar (J)_(C^('))+Ad^(2)
where I_(x) is the area's moment of inertia about the noncentroidal x axis,
()/(bar) (I)_(x^(')) is the moment of inertia about the centroidal x axis, A is the total
area, d_(y) is the perpendicular distance in the y direction between the
centroid and the x axis, I_(y) is the area's moment of inertia about the
noncentroidal y axis, ()/(bar) (I)_(y^(')) is the moment of inertia about the centroidal y
axis, d_(x) is the perpendicular distance in the x direction between the
centroid and the y axis, J_(O) is the polar moment of inertia about some
noncentroidal point, ()/(bar) (J)_(C) is the polar moment of inertia about the centroid,
and d is the distance between the points O and C.
Figure
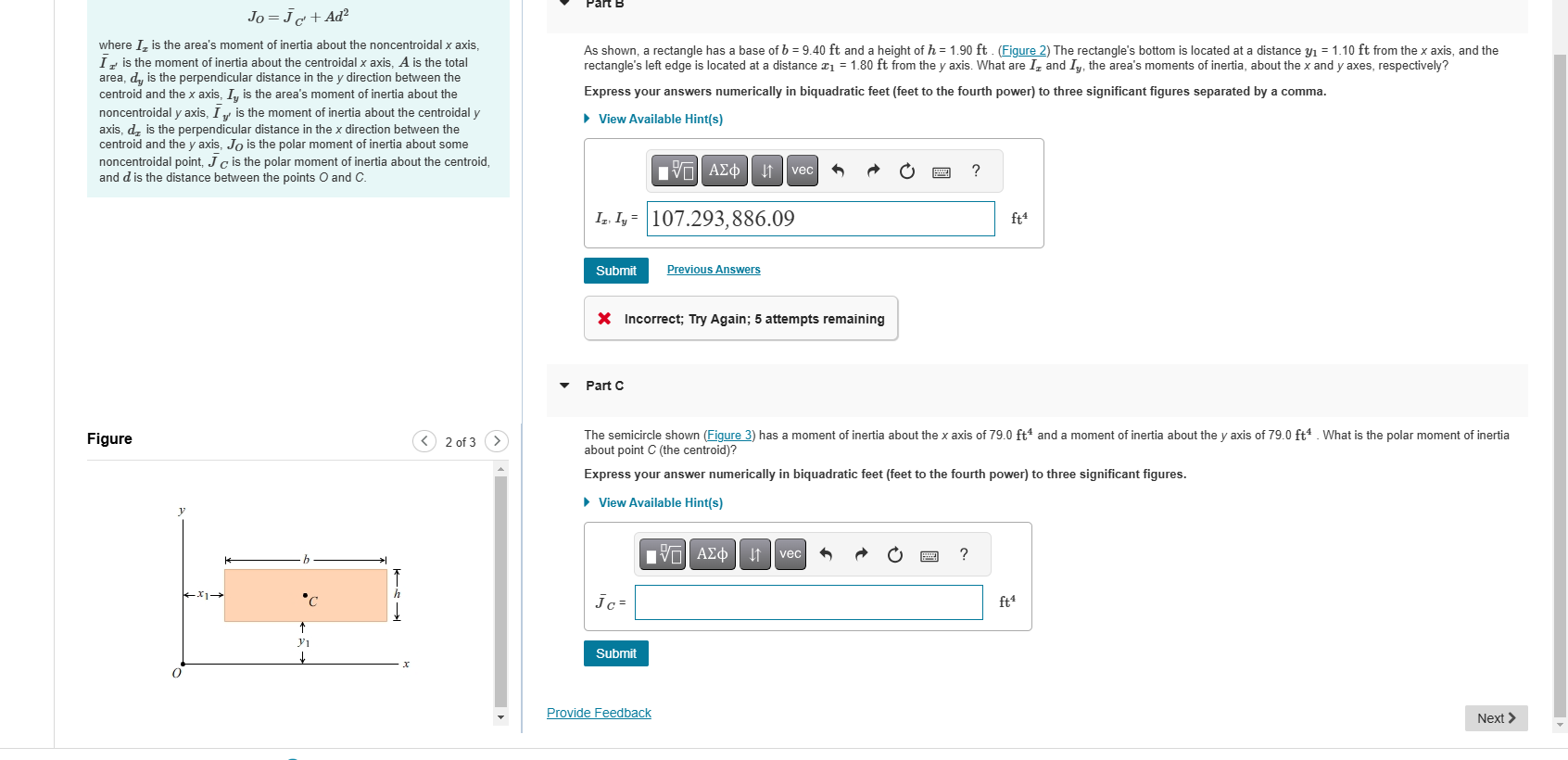
As shown, a rectangle has a base of b=9.40ft and a height of h=1.90ft. (Figure 2) The rectangle's bottom is located at a distance y_(1)=1.10ft from the x axis, and the
rectangle's left edge is located at a distance x_(1)=1.80ft from the y axis. What are I_(x) and I_(y), the area's moments of inertia, about the x and y axes, respectively?
Express your answers numerically in biquadratic feet (feet to the fourth power) to three significant figures separated by a comma.
View Available Hint(s)
Incorrect; Try Again; 5 attempts remaining
Part C
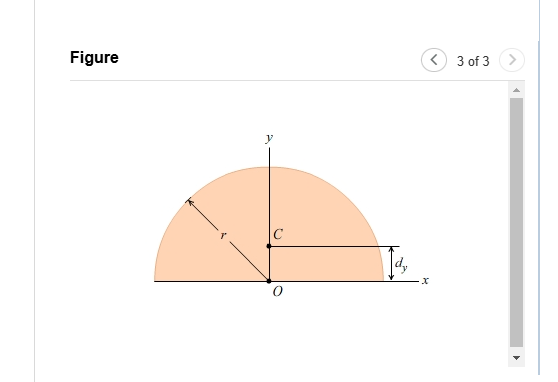
The semicircle shown (Figure 3) has a moment of inertia about the x axis of 79.0ft^(4) and a moment of inertia about the y axis of 79.0ft^(4). What is the polar moment of inertia
about point C (the centroid)?
Express your answer numerically in biquadratic feet (feet to the fourth power) to three significant figures.
View Available Hint(s) Figure
3 of 3