(Solved): In the Figure, . Find Vector components for F1x, F2x,F2y,F2z,F3x,F3z. F1 =80 N, F2 =140N, F3=200 ...

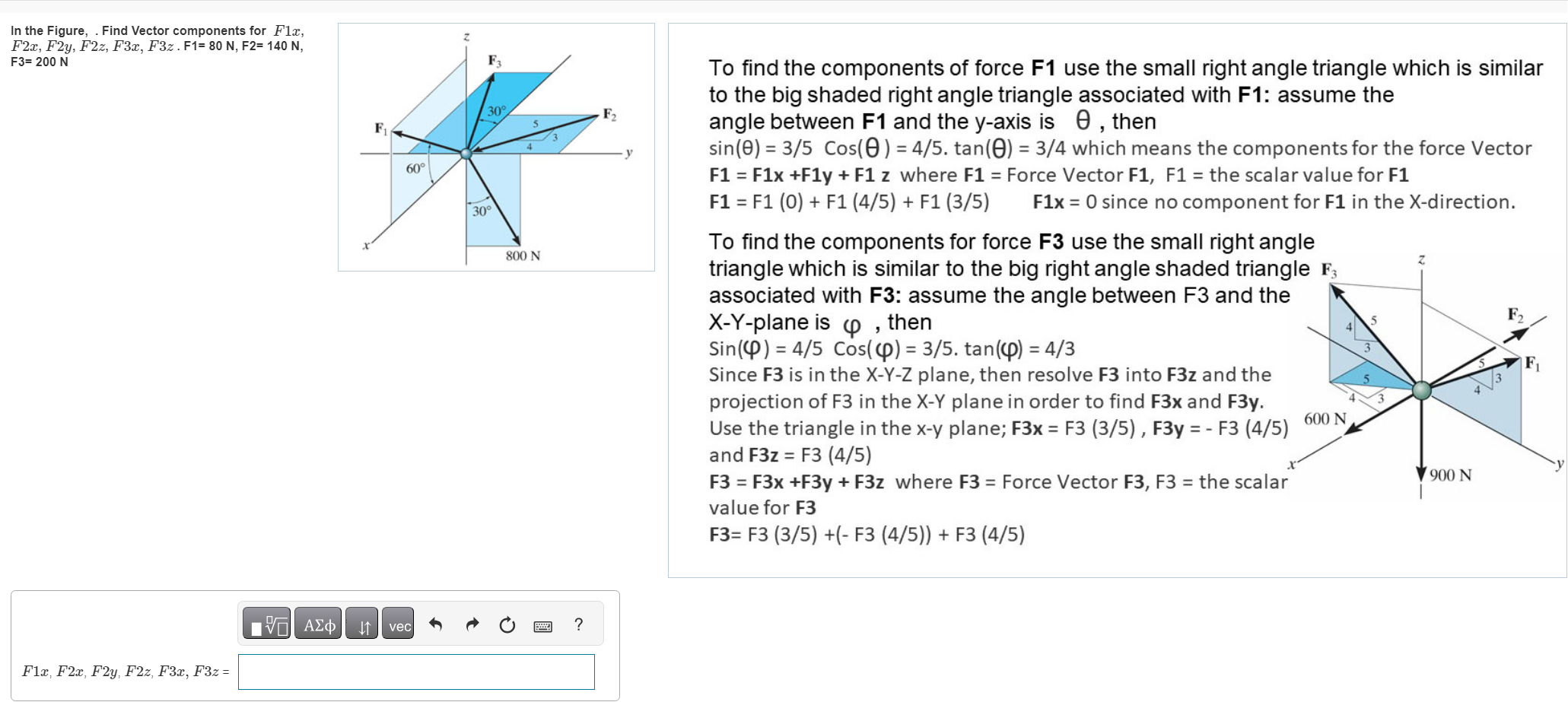
In the Figure, . Find Vector components for $F1x$, $F2x,F2y,F2z,F3x,F3z$. F1 $=80$ N, F2 $=140\mathrm{N}$, $\mathrm{F}3=200\mathrm{N}$ To find the components of force $F1$ use the small right angle triangle which is similar to the big shaded right angle triangle associated with F1: assume the angle between $F1$ and the $y$-axis is $?$, then $\sin (?)=3/5\cos (?)=4/5?\tan (?)=3/4$ which means the components for the force Vector $F1=F1x+F1y+F1z$ where $F1=$ Force Vector F1, F1 = the scalar value for F1 $F1=F1(0)+F1(4/5)+F1(3/5)F1x=0$ since no component for F1 in the X-direction. To find the components for force $F3$ use the small right anç $0$ triangle which is similar to the big right angle shaded triang associated with F3: assume the angle between $\mathrm{F}3$ and the $\mathrm{X}$-Y-plane is $?$, then $\mathrm{Sin}(?)=4/5\mathrm{Cos}(?)=3/5?\tan (?)=4/3$ Since $F3$ is in the $X?Y?Z$ plane, then resolve $F3$ into $F3z$ and the projection of $F3$ in the $X?Y$ plane in order to find F3x and F3y. Use the triangle in the $x?y$ plane; $F3x=F3(3/5),F3y=?F3(4/5)$ and $\mathrm{F}3\mathrm{z}=\mathrm{F}3(4/5)$ $F3=F3x+F3y+F3z$ where $F3=$ Force Vector F3, F3 = the scalar value for $F3$ $F3=F3(3/5)+(?F3(4/5))+F3(4/5)$