(Solved): In the circuit shown in Fig. 1,T is s practical transformer whose turns ratio n1 ...

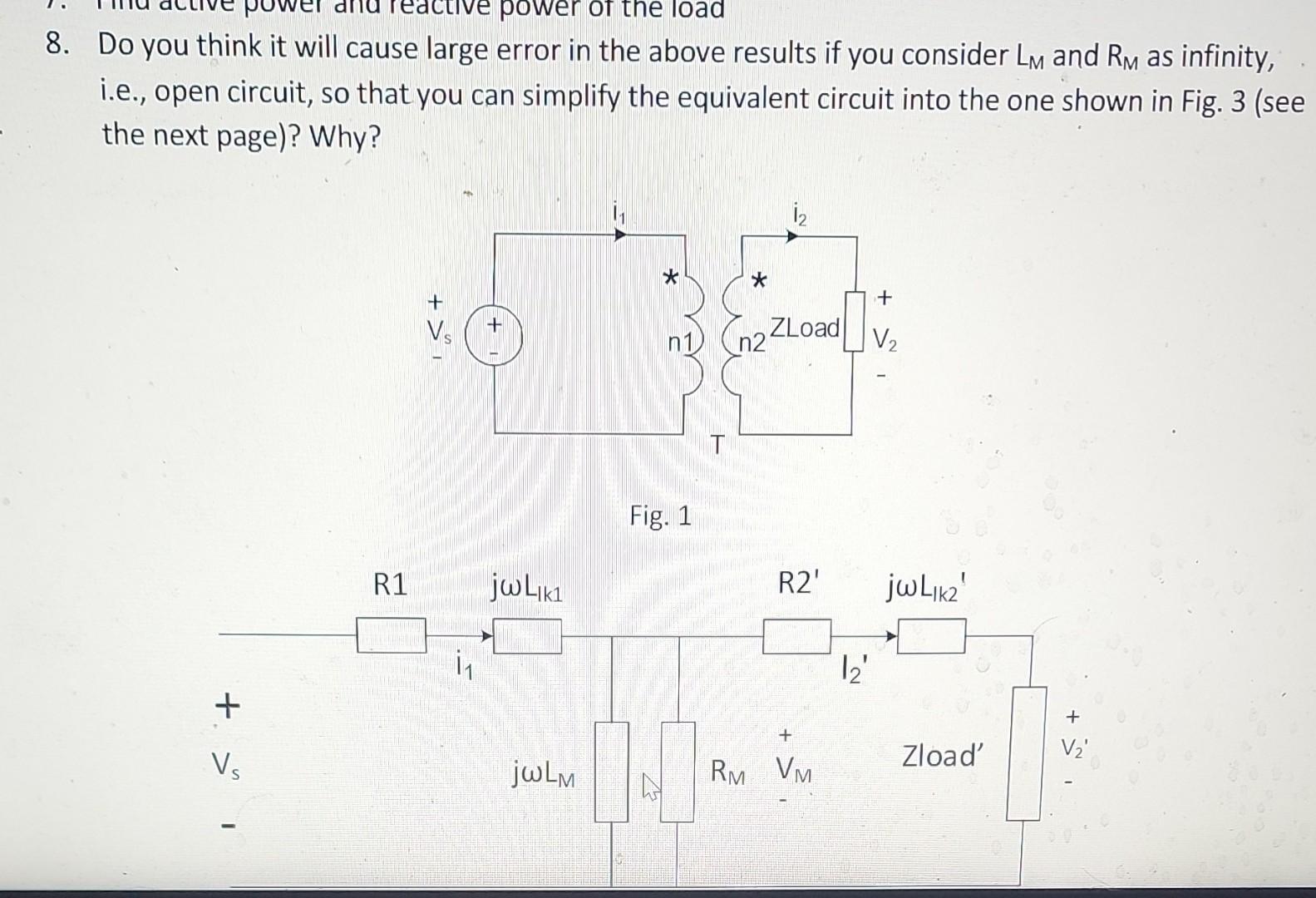
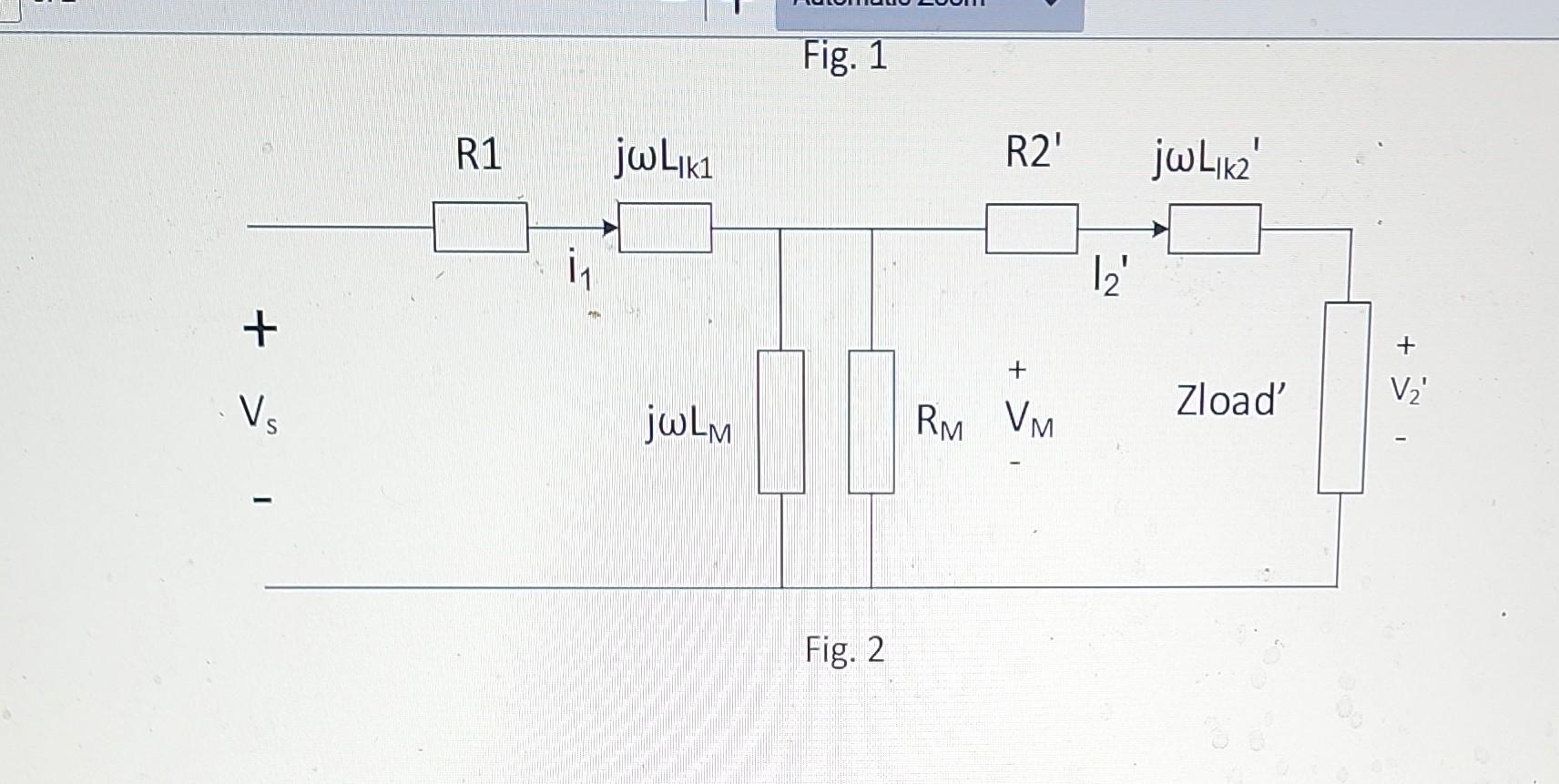
In the circuit shown in Fig. $$1,\mathrm{T}$$ is s practical transformer whose turns ratio $${\mathrm{n}}_1/{\mathrm{n}}_2$$ is 2 , where $${\mathrm{n}}_1$$ and $${\mathrm{n}}_2$$ are the number of turns of the primary winding and the number of turns of the secondary winding, respectively; $${\mathrm{V}}_{\mathrm{s}}$$ is a sinusoidal voltage source whose phasor voltage is \( 240 \mathrm{v} 2\left\llcorner 45^{\circ} \mathrm{V}\right. \) and whose frequency is $$60\mathrm{Hz}$$; Zload represents the load of the transformer and is made of a $$0.4?$$ resistor in series with a $$0.5\mathrm{mH}$$ inductor. Fig. 2 shows the equivalent circuit of the transformer and the load reflected to the primary side. In the circuit, $$R1=0.01?;L_{k1}=10?H;L_M=100\mathrm{mH};R_M=100?;R{2}^{?}=0.02?;L_{k2}{}^{?}=15?\mathrm{H}$$. 1. Find Zload', the impedance of the load transferred to the primary side (Hint: recall impedance transfer for an ideal transformer) 2. Find phasor current $$I1$$ 3. Find phasor voltage $$V_M$$ 4. Find phasor current 12' 5. Find power loss of the transformer, i.e., total active power of $$R1,R{2}^{?}$$, and $$R_M$$ 6. Find total reactive power absorbed by the transformer, i.e., total reactive power of $$L_{k1},L_{kk2}$$, and $$L_M$$ 7. 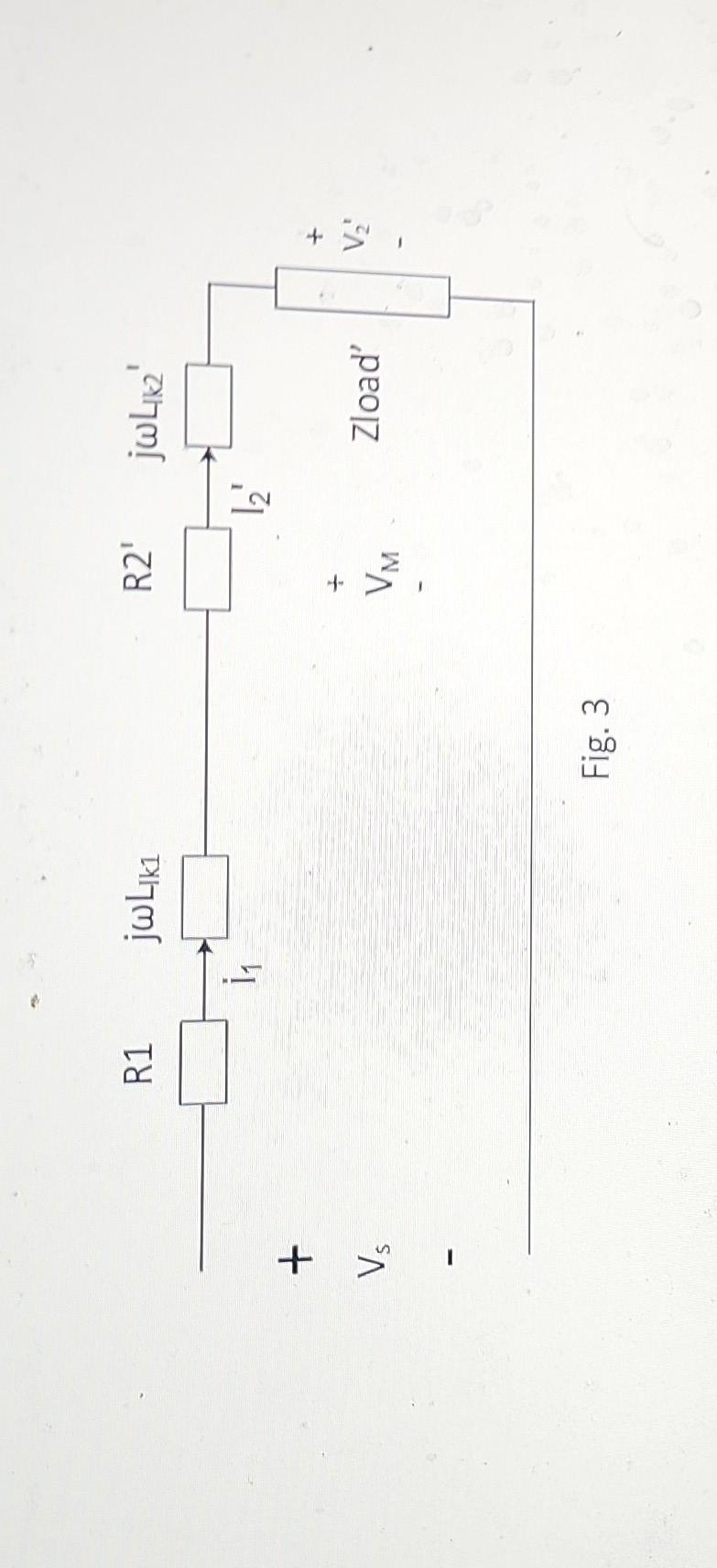Find active power and reactive power of the load 8. Do you think it will cause large error in the above results if you consider $$L_M$$ and $$R_M$$ as infinity, i.e., open circuit, so that you can simplify the equivalent circuit into the one shown in Fig. 3 (see the next page)? Why? Fig. 1 Fig. 1 Fig. 2 Fig. 3