(Solved): In the circuit shown below, the switch in the circuit is moved, as shown, from open to close at \( ...

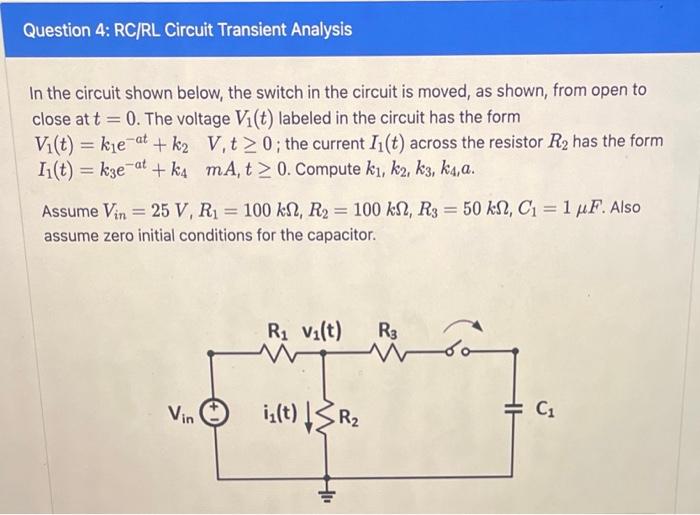
In the circuit shown below, the switch in the circuit is moved, as shown, from open to close at \( t=0 \). The voltage \( V_{1}(t) \) labeled in the circuit has the form \( V_{1}(t)=k_{1} e^{-a t}+k_{2} \quad V_{1} t \geq 0 \); the current \( I_{1}(t) \) across the resistor \( R_{2} \) has the form \( I_{1}(t)=k_{3} e^{-a t}+k_{4} \quad m A, t \geq 0 \). Compute \( k_{1}, k_{2}, k_{3}, k_{4}, a \). Assume \( V_{i n}=25 V, R_{1}=100 k \Omega, R_{2}=100 k \Omega, R_{3}=50 k \Omega, C_{1}=1 \mu F \). Also assume zero initial conditions for the capacitor. 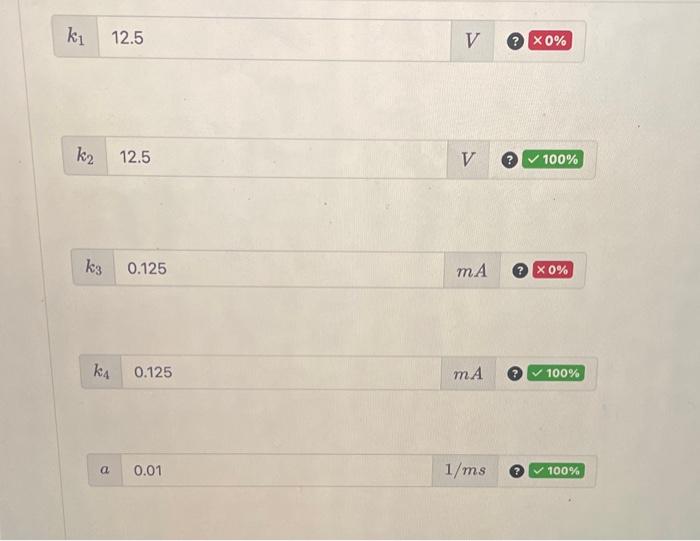\begin{tabular}{l|l} \hline\( k_{1} \) & \( 12.5 \) \\ \hline \end{tabular} \begin{tabular}{l|lll} \hline\( k_{2} \) & \( 12.5 \) & \( V \) & (3 \( \checkmark 100 \% \) \\ \hline \end{tabular} \begin{tabular}{|l|l|l|l} \hline\( k_{3} \) & \( 0.125 \) & \( m A \) & (3) \( \times 0 \% \) \\ \hline \end{tabular} \begin{tabular}{|c|c|c|c|} \hline\( k_{4} \) & \( 0.125 \) & \( m A \) & ( ? 100\% \\ \hline & & & \\ \hline\( a \) & \( 0.01 \) & \( 1 / m s \) & O \( \sqrt{100 \%} \) \\ \hline \end{tabular}