Home /
Expert Answers /
Mechanical Engineering /
in-a-salvador-dali-painting-a-silver-dinner-tray-has-grown-legs-and-starts-running-with-a-bowling-pa904
(Solved): In a Salvador Dali painting, a silver dinner tray has grown legs and starts running with a bowling ...
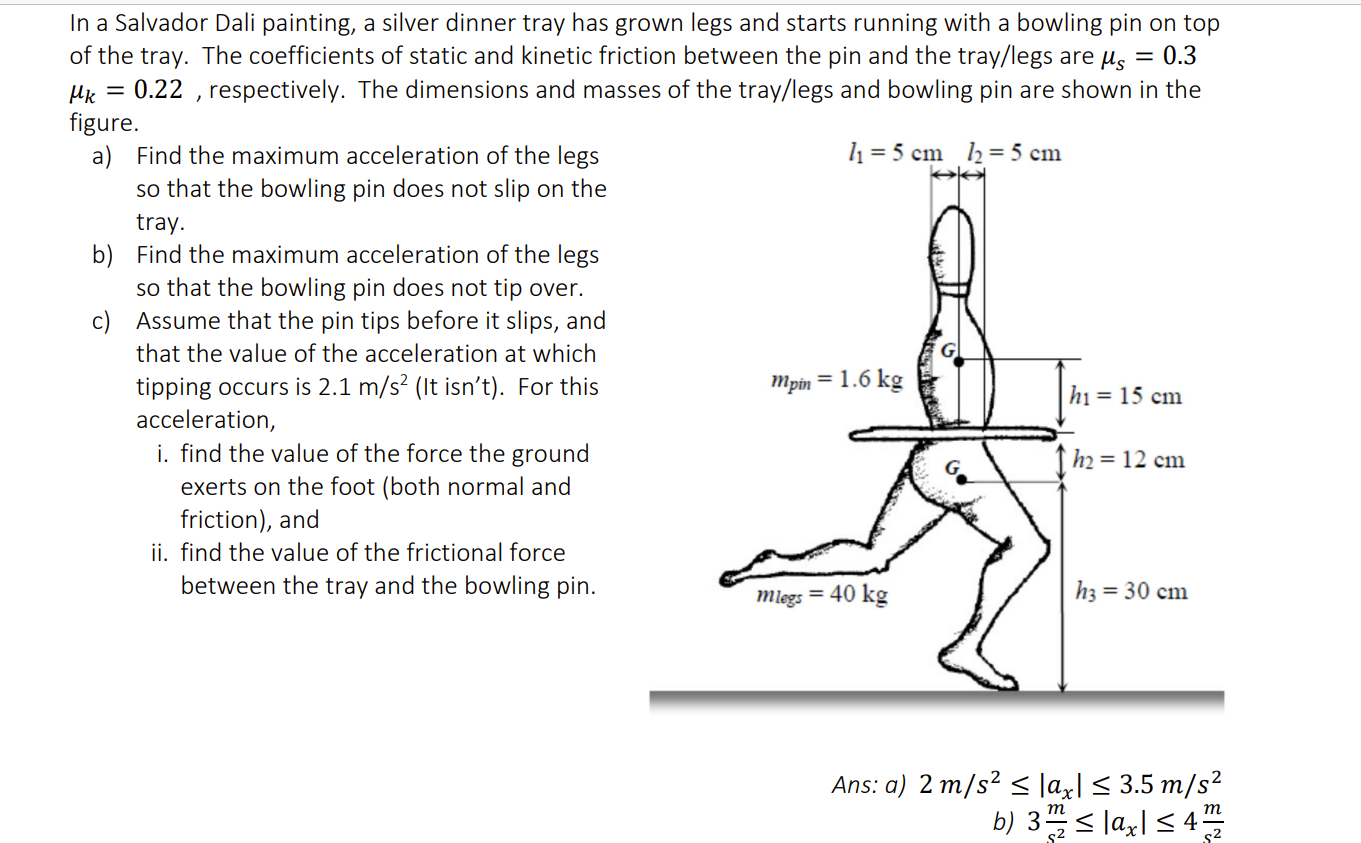
In a Salvador Dali painting, a silver dinner tray has grown legs and starts running with a bowling pin on top of the tray. The coefficients of static and kinetic friction between the pin and the tray/legs are , respectively. The dimensions and masses of the tray/legs and bowling pin are shown in the figure. a) Find the maximum acceleration of the legs so that the bowling pin does not slip on the tray. b) Find the maximum acceleration of the legs so that the bowling pin does not tip over. c) Assume that the pin tips before it slips, and that the value of the acceleration at which tipping occurs is (It isn't). For this acceleration, i. find the value of the force the ground exerts on the foot (both normal and friction), and ii. find the value of the frictional force between the tray and the bowling pin. Ans: a) b)
Expert Answer
To solve this problem, we need to apply the laws of statics and dynamics to the system consisting of the tray with legs and the bowling pin. a) To find the maximum acceleration of the legs so that the bowling pin does not slip on the tray, we need to use the coefficient of static friction. The maximum acceleration is given by: where g is the acceleration due to gravity (9.8 m/s^2). Substituting the values given, we get: However, we need to make sure that the bowling pin does not slip in any direction. Since the tray is moving horizontally, we need to consider the maximum acceleration in the horizontal direction as well. The maximum horizontal acceleration is given by: where is the coefficient of static friction between the tray and the legs. Substituting the values given, we get: