Home /
Expert Answers /
Calculus /
how-and-why-did-they-get-the-radius-of-12-to-equal-72pi-below-a-circular-plate-is-submerged-in-wat-pa393
(Solved): HOW and WHY did they get the radius of 12 to equal 72pi? Below, a circular plate is submerged in wat ...
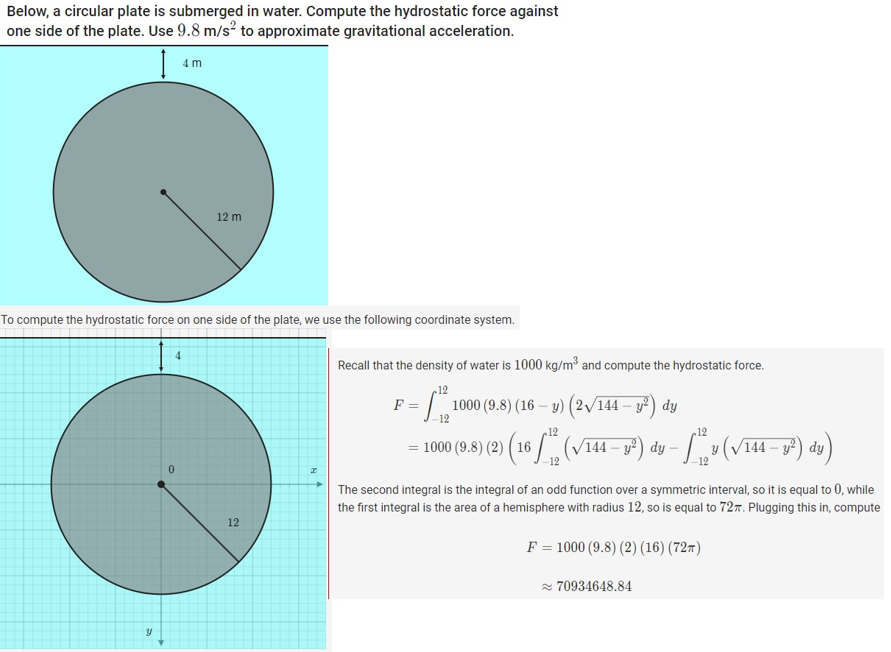
HOW and WHY did they get the radius of 12 to equal 72pi?
Below, a circular plate is submerged in water. Compute the hydrostatic force against one side of the plate. Use to approximate gravitational acceleration. To compute the hydrostatic force on one side of the plate, we use the following coordinate system. Recall that the density of water is and compute the hydrostatic force. The second integral is the integral of an odd function over a symmetric interval, so it is equal to 0 , while the first integral is the area of a hemisphere with radius 12 , so is equal to . Plugging this in, compute
Expert Answer
To evaluate the given integral, need to split it into two separate integrals as shown: Let; Let's...