(Solved): Here is the output of a linear regression to estimate the welght of a 12-year-old child (in pounds) ...

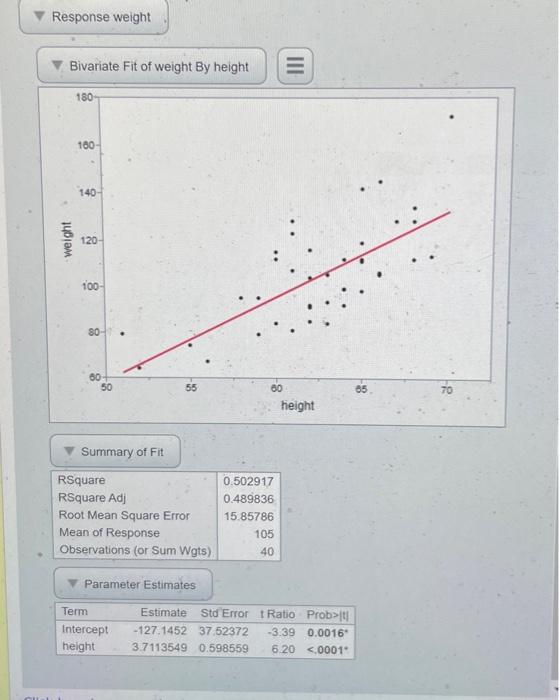
Here is the output of a linear regression to estimate the welght of a 12-year-old child (in pounds), given their height (in Inches), A regrasaion output fias aiso been diven. Use the MP applet to answer the questions besow. Response weight Bivariate Fit of weight By height Summary of Fit \begin{tabular}{|l|r|} \hline RSquare & \( 0.502917 \) \\ RSquare Adj & \( 0.489836 \) \\ Root Mean Square Error & \( 15.85786 \) \\ Mean of Response & 105 \\ Observations (or Sum Wgts) & 40 \\ \hline \end{tabular} Parameter Estimates \begin{tabular}{|lrrrr|} \hline Term & Estimate & Std Error & \( t \) Ratio & Prob> \( |t| \) \\ \hline Intercept & \( -127.1452 \) & \( 37.52372 \) & \( -3.39 \) & \( 0.0016^{*} \) \\ height & \( 3.7113549 \) & \( 0.598559 \) & \( 6.20 \) & \( <.0001^{*} \) \\ \hline \end{tabular} 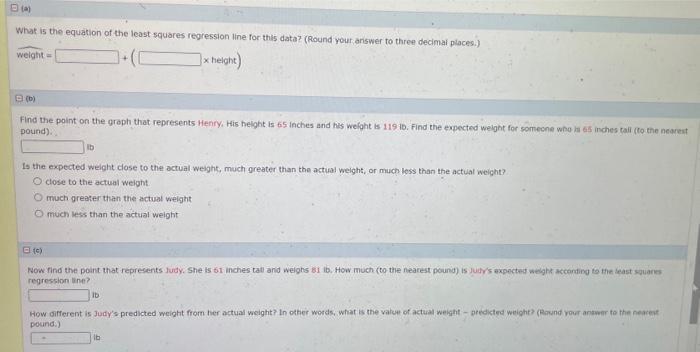What is the equation of the least squores regression line for this data? (Round your answer to three decimai places.) \[ \overline{\text { weight }}= \] (b) Find the point on the greph that represents Henry, His height is 65 inches and his welght is 11910 . Find the expected welght for someone who in 65 inches tail (to the neareat pound). Is the expected welght close to the actual weight, much greater than the actual welght, or much less than the actual weight? close to the actual weight. much greater than the actual weight much less than the actual weight (c) Now find the point that represents fudy. She is 61 inches tat and weighs 81 lb. How much (to the hearest pounid) is luet's axpected weight acconding to the least spuares regression line? Ib. How different is Judy's predicted weight from her actual weight? In other words, what is the value of actual weight - predicted weight? 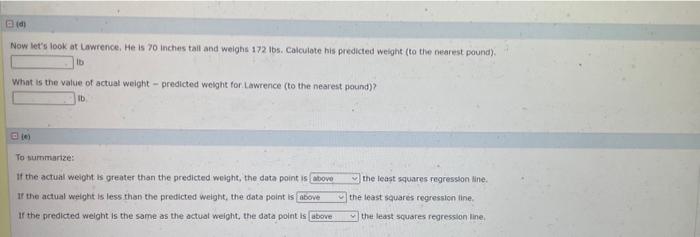(Raund your antwer to the neacest pound.) Now let's look at Lawrence, He is 70 inches tail and weighs \( 172 \mathrm{lbs} \). Calculate his predicted weight (to the nearest pound). its What is the value of actual weight - predicted weight for Lawrence (to the nearest pound)? ib (8) To surmmarize: If the actual weight is greater than the predicted weight, the data point is the least squares regression Nine. If the actual welight is less than the predicted weight, the data point is the least squares regression line. If the predicted welght is the same as the actual weight, the data point is the least squares regression line.