(Solved): help 8. Consider an inverted conical tank that is being filled with water. The tank's radius is \( 2 ...

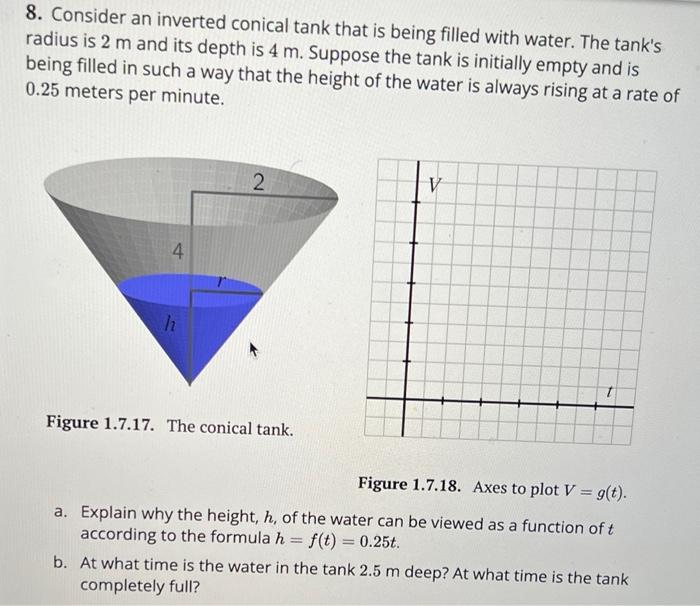
8. Consider an inverted conical tank that is being filled with water. The tank's radius is \( 2 \mathrm{~m} \) and its depth is \( 4 \mathrm{~m} \). Suppose the tank is initially empty and is being filled in such a way that the height of the water is always rising at a rate of \( 0.25 \) meters per minute. Figure 1.7.17. The conical tank. Figure 1.7.18. Axes to plot \( V=g(t) \). a. Explain why the height, \( h \), of the water can be viewed as a function of \( t \) according to the formula \( h=f(t)=0.25 t \). b. At what time is the water in the tank \( 2.5 \mathrm{~m} \) deep? At what time is the tank completely full? c. Suppose we think of the volume, \( V \), of water in the tank as a function of \( t \) and name the function \( V=g(t) \). Do you expect that the function \( g \) has an inverse function? Why or why not? d. Recall that the volume of a cone of radius \( r \) and height \( h \) is \( V=\frac{\pi}{3} r^{2} h \). Due to the shape of the tank, similar triangles tell us that \( r \) and \( h \) satisfy the proportion \( r=\frac{1}{2} h \), and thus \[ V=\frac{\pi}{3}\left(\frac{1}{2} h\right)^{2} h=\frac{\pi}{12} h^{3} \] Use the fact that \( h=f(t)=0.25 t \) along with Equation (1.7.1) to find \( a \) formula for \( V=g(t) \). Sketch a plot of \( V=g(t) \) on the blank axes provided in Figure 1.7.18. Write at least one sentence to explain why \( V=g(t) \) has the shape that it does. e. Take the formula for \( V=g(t) \) that you determined in (d) and solve for \( t \) to determine a formula for \( t=g^{-1}(V) \). What is the meaning of the formula you find? f. Find the exact time that there is \( \frac{8}{3} \pi \) cubic meters of volume in the tank.