(Solved): GOAL Apply kinematics to horizontal motion with two phases. PROBLEM A typical jetliner lands at a s ...

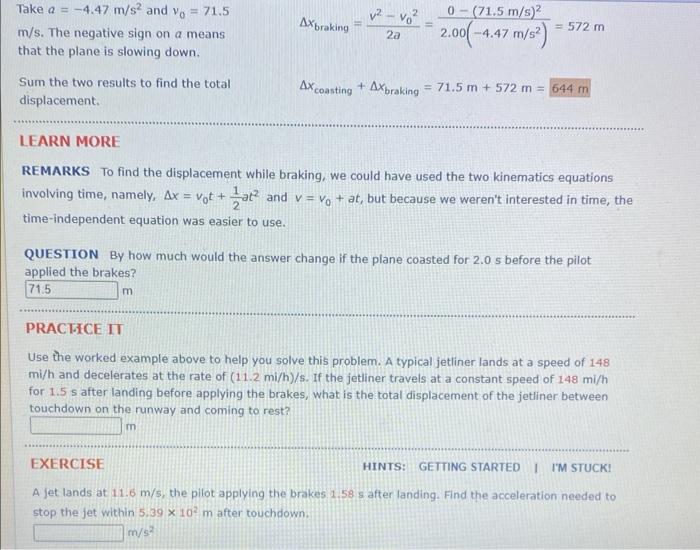
GOAL Apply kinematics to horizontal motion with two phases. PROBLEM A typical jetliner lands at a speed of \( 1.60 \times 10^{2} \) \( \mathrm{mi} / \mathrm{h} \) and decelerates at the rate of \( (10 \mathrm{mi} / \mathrm{h}) / \mathrm{s} \). If the plane travels at a constant speed of \( 1.60 \times 10^{2} \mathrm{mi} / \mathrm{h} \) for \( 1.00 \mathrm{~s} \) after Coasting and braking distances for a landing jecliner: landing before applying the brakes, what is the total displacement of the aircraft between touctidown on the runway and coming to rest? STRATEGY First, convert all quantities to SI units. The problem must be solved in two parts, or phases, corresponding to the initial coast after touchdown, followed by braking. Using the kinematic equations, find the displacement during each part and add the two displacements. SOLUIION Convert units of speed and acceleration to SI. \[ \begin{array}{l} v_{0}=\left(1.60 \times 10^{2} \mathrm{mi} / \mathrm{h}\right)\left(\frac{0.447 \mathrm{~m} / \mathrm{s}}{1.00 \mathrm{mi} / \mathrm{h}}\right)=71.5 \mathrm{~m} / \mathrm{s} \\ \Rightarrow=(-10.0(\mathrm{mi} / \mathrm{h}) / \mathrm{s})\left(\frac{0.447 \mathrm{~m} / \mathrm{s}}{1.00 \mathrm{mi} / \mathrm{h}}\right)=-4.47 \mathrm{~m} / \mathrm{s}^{2} \end{array} \] Taking \( a=0, v_{0}=71.5 \mathrm{~m} / \mathrm{s} \), and \( t_{i}= \) \( 1.00 \mathrm{~s} \), find the displacement while the plane is coasting. Use the time-independent kinematic equation to find the displacement while the plane is braking. Take \( a=-4.47 \mathrm{~m} / \mathrm{s}^{2} \) and \( v_{0}=71.5 \) \( \mathrm{m} / \mathrm{s} \). The negative sign on a means that the plane is slowing down. \( \Delta x_{\text {braking }}=\frac{v^{2}-v_{0}^{2}}{2 a}=\frac{0-(71.5 \mathrm{~m} / \mathrm{s})^{2}}{2.00\left(-4.47 \mathrm{~m} / \mathrm{s}^{2}\right)}=572 \mathrm{~m} \) Sum the two results to find the total displacement. \[ \Delta x_{\text {coasting }}+\Delta x_{\text {braking }}=71.5 m+572 m= \] IEARN MORE REMARKS To find the displacement while braking, we could have used the two kinematics equations involving time, namely, \( \Delta x=v_{0} t+\frac{1}{2} a t^{2} \) and \( v=v_{0}+a t \), but because we weren't interested in time, the time-independent equation was easier to use. QUESTION By how much would the answer change if the plane coasted for \( 2.0 \) s before the pilot applied the brakes? PRACIICEII Use the worked example above to help you solve this problem. A typical jetliner lands at a speed of 148 . \( \mathrm{mi} / \mathrm{h} \) and decelerates at the rate of \( (11.2 \mathrm{mi} / \mathrm{h}) / \mathrm{s} \). If the jetliner travels at a constant speed of \( 148 \mathrm{mi} / \mathrm{h} \) for \( 1.5 \mathrm{~s} \) after landing before applying the brakes, what is the total displacement of the jetliner between touchdown on the runway and coming to rest? EXERCISE HINTS: GETTING STARTED I A jet lands at \( 11.6 \mathrm{~m} / \mathrm{s} \), the pilot applying the brakes. \( 1.58 \mathrm{~s} \) after landing. Find the acceleration needed to stop the jet within \( 5.39 \times 10^{2} \mathrm{~m} \) after touchdown. \[ \mathrm{m} / \mathrm{s}^{2} \]