(Solved): Given a solution of 0.300 M HEPES in its fully protonated form, and ready access to&n ...

Given a solution of 0.300 M HEPES in its fully protonated form, and ready access to 0.250 M HCl, 0.250 M NaOH and distilled water, complete the questions below to describe the preparation of 1 L of 0.0400 M HEPES buffer solution at pH 7.70
.

 

 

 

 

Need help with D

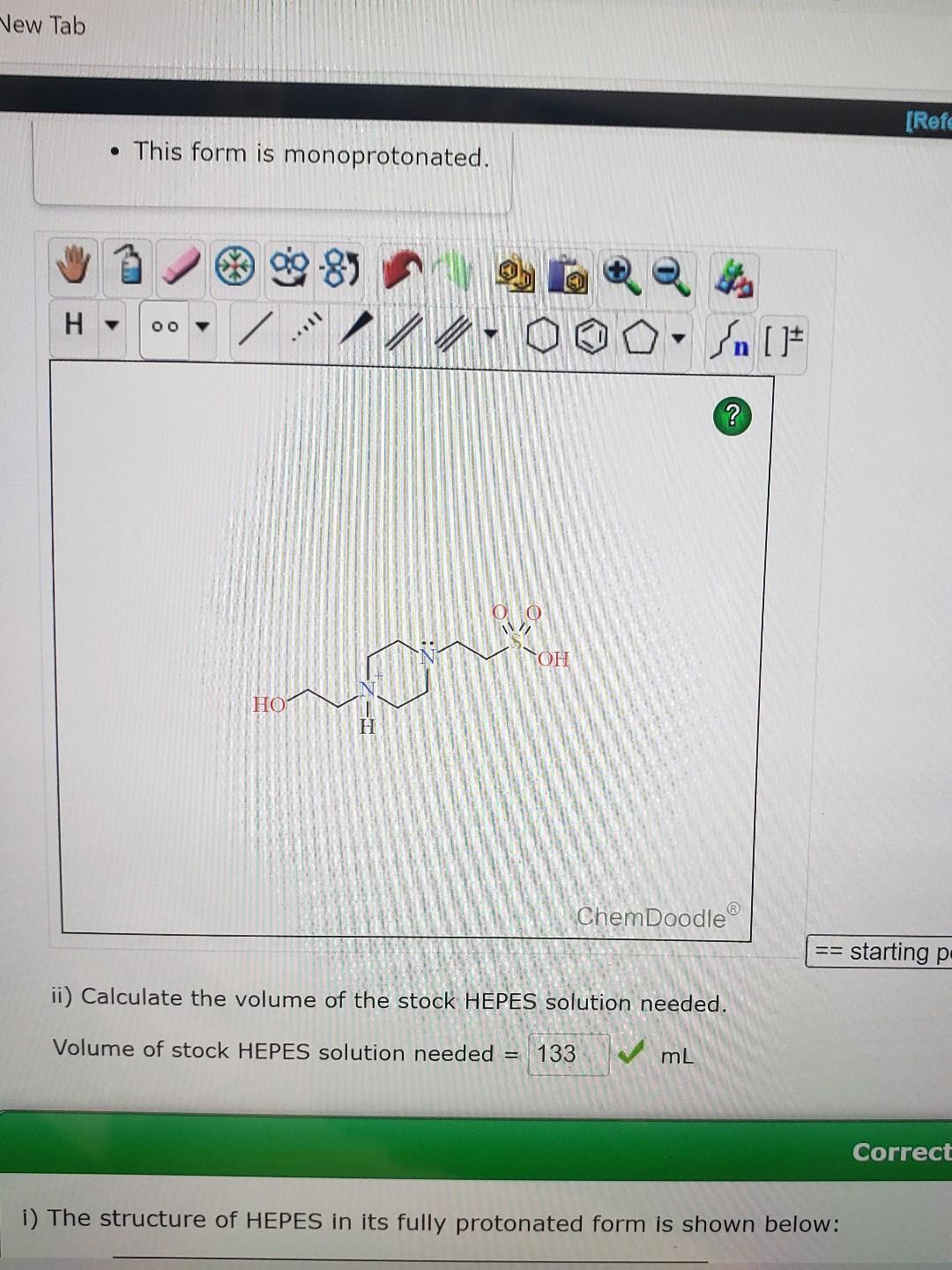
- This form is monoprotonated. ii) Calculate the volume of the stock HEPES solution needed. Volume of stock HEPES solution needed = \( \mathrm{mL} \) i) The structure of HEPES in its fully protonated form is shown below: \( \frac{\left[\mathrm{HEPES}^{1-}\right]}{[\mathrm{HEPES}-\mathrm{H}]}= \) ii) Calculate the concentration of HEPES-H in the final buffer solution. Concentration of HEPES-H in the final buffer solution = iii) Calculate the concentration of HEPES \( ^{1-} \) in the final buffer solution. Concentration of HEPES \( { }^{1-} \) in the final buffer solution = Correct atio of concentrations he ratio of the concentrations of \( \mathrm{HEPES}^{1-} \) and \( \mathrm{HEPES}-\mathrm{H} \) in the final buffer solution can be calculated from the \( \mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log _{10}\left(\frac{\left[\mathrm{HEPES}^{1-}\right]}{[\mathrm{HEPES}-\mathrm{H}]}\right) \) \( 7.70=7.55+\log _{10}\left(\frac{\left[\mathrm{HEPES}^{1-}\right]}{[\mathrm{HEPES}-\mathrm{H}]}\right) \) \( \mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log _{10}\left(\frac{\left[\mathrm{HEPES}^{1-}\right]}{\left[\mathrm{HEPES}^{-\mathrm{H}]}\right]}\right) \) Concentrations of HEPES \( { }^{1-} \) and HEPES-H relationship is also true: \( \left[\right. \) HEPES \( \left.^{1-}\right]+[ \) HEPES-H \( ]=0.0400 M \) Isolating [HEPES-H], and substituting into the equation above gives: \[ \left[\mathrm{HEPES}^{1-}\right]+\frac{\left[\text { HEPES }^{-1}\right]}{1.41}=0.0400 \mathrm{M} \] Solving this gives a concentration of \( 0.0234 \mathrm{M} \) in the final buffer solution. The concentration of HEPES-H in the final buffer solution is found using: \( \left[\mathrm{HEPES}^{1-}\right]+[\mathrm{HEPES}-\mathrm{H}]=0.0400 M \) \( [\mathrm{HEPES}-\mathrm{H}]=0.0166 \mathrm{M} \) i) Calculate the total volume of \( 0.250 \mathrm{M} \mathrm{NaOH} \) that needs to be added to make the buffer system. lelatiolisilip is disu ulue: \[ \left[\mathrm{HEPES}^{1-}\right]+[\mathrm{HEPES}-\mathrm{H}]=0.0400 M \] Isolating [HEPES-H], and substituting into the equation above gives: \[ \left[\mathrm{HEPES}^{1-}\right]+\frac{\left[\mathrm{HEPES}^{-1}\right]}{1.41}=0.0400 \mathrm{M} \] Solving this gives a concentration of \( \mathbf{0 . 0 2 3 4} \mathrm{M} \) in the final buffer solution. The concentration of HEPES-H in the final buffer solution is found using: \( \left[\mathrm{HEPES}{ }^{1-}\right]+[\mathrm{HEPES}-\mathrm{H}]=0.0400 \mathrm{M} \) \( [\mathrm{HEPES}-\mathrm{H}]=0.0166 M \) (1) Calculate the total volume of \( 0.250 \mathrm{M} \mathrm{NaOH} \) that needs to be added to make the buffer system. \( \mathrm{mL} \) ii) Calculate the volume of distilled water that needs to be added to make the solution up to \( 1 \mathrm{~L} \). \( \mathrm{mL} \)