(Solved): From the below graph, estimate the true stress ' \( \sigma_{T}{ }^{\prime} \) and true strain' \( \ ...

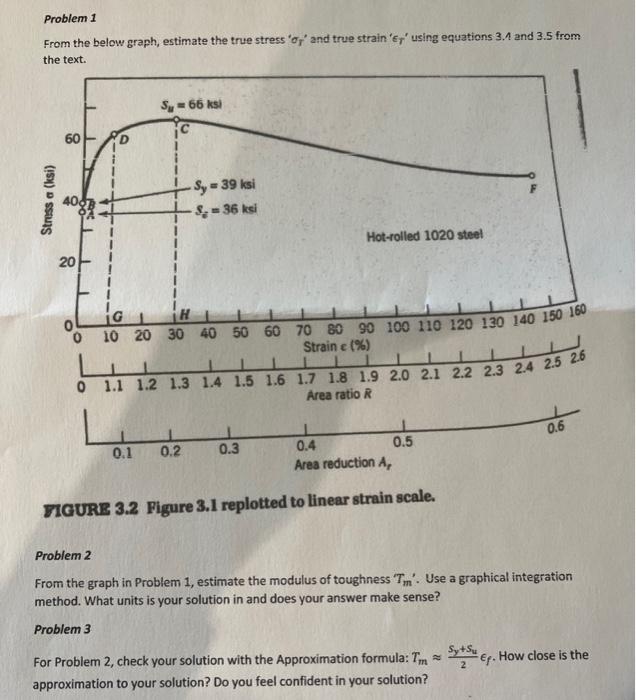
From the below graph, estimate the true stress ' \( \sigma_{T}{ }^{\prime} \) and true strain' \( \epsilon_{T} \) ' using equations \( 3.1 \) and \( 3.5 \) from HCURE 3.2 Figure \( 3.1 \) replotted to linear strain scale. Problem 2 From the graph in Problem 1, estimate the modulus of toughness ' \( T_{m} \). Use a graphical integration method. What units is your solution in and does your answer make sense? Problem 3 For Problem 2, check your solution with the Approximation formula: \( T_{m} \approx \frac{s_{y}+S_{u}}{2} \epsilon_{\rho} \). How close is the approximation to your solution? Do you feel confident in your solution? Problem I \[ \begin{array}{l} \sigma_{T}=\left(P / A_{0}\right)(1+\epsilon)=\sigma(1+\epsilon)=\sigma R \\ E_{T}=\sum_{L_{0}}^{L} \frac{\Delta L}{L}=\ln R=\ln (1+\epsilon) \end{array} \] Problem 2 \[ T_{m}=\int_{0}^{\varepsilon} \sigma d \varepsilon \quad T_{m}=\frac{S_{u}+S_{u}}{2} \epsilon_{f} \]