(Solved): First write the given homogeneous system in the matrix form \( A x=0 \). Then find the solution in ...

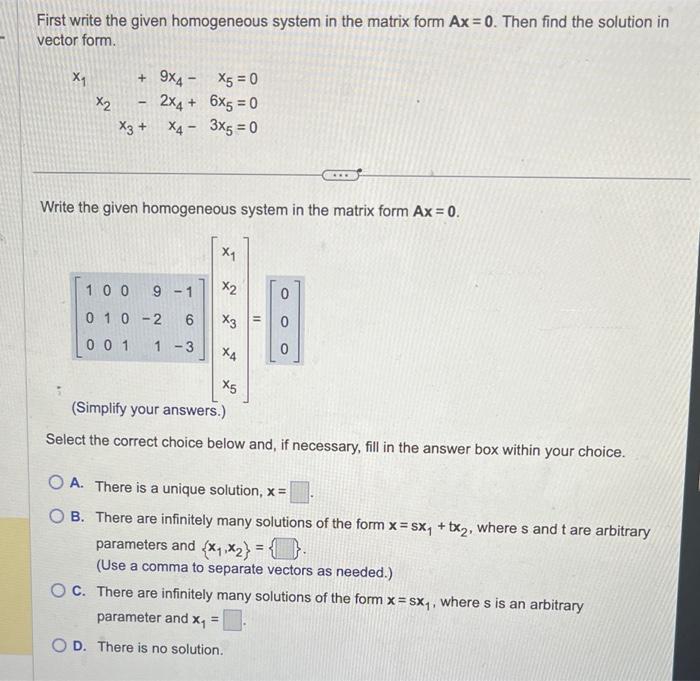
First write the given homogeneous system in the matrix form \( A x=0 \). Then find the solution in vector form. \[ \begin{array}{r} x_{1}+9 x_{4}-x_{5}=0 \\ x_{2}-2 x_{4}+6 x_{5}=0 \\ x_{3}+x_{4}-3 x_{5}=0 \end{array} \] Write the given homogeneous system in the matrix form \( A x=0 \). Select the correct choice below and, if necessary, fill in the answer box within your choice. A. There is a unique solution, \( x= \) B. There are infinitely many solutions of the form \( x=s x_{1}+t x_{2} \), where \( s \) and \( t \) are arbitrary parameters and \( \left\{x_{1}, x_{2}\right\}= \). (Use a comma to separate vectors as needed.) C. There are infinitely many solutions of the form \( \mathbf{x}=s \mathbf{x}_{1} \), where \( s \) is an arbitrary parameter and \( \mathbf{x}_{1}= \) D. There is no solution. 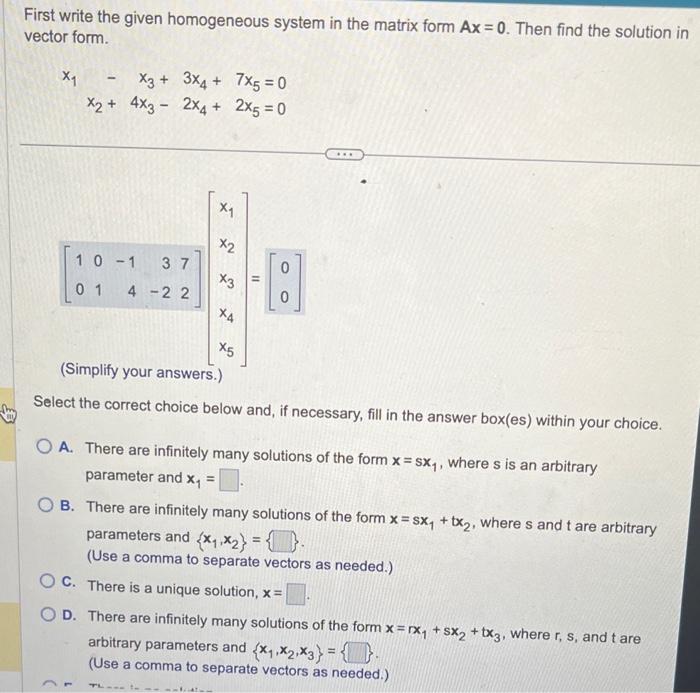First write the given homogeneous system in the matrix form \( A x=0 \). Then find the solution in vector form. \[ \begin{array}{r} x_{1}-x_{3}+3 x_{4}+7 x_{5}=0 \\ x_{2}+4 x_{3}-2 x_{4}+2 x_{5}=0 \end{array} \] (Simplify your answers.) Select the correct choice below and, if necessary, fill in the answer box(es) within your choice. A. There are infinitely many solutions of the form \( x=s x_{1} \), where \( s \) is an arbitrary parameter and \( \mathrm{x}_{1}= \) B. There are infinitely many solutions of the form \( x=s x_{1}+t x_{2} \), where \( s \) and \( t \) are arbitrary parameters and \( \left\{x_{1}, x_{2}\right\}= \). (Use a comma to separate vectors as needed.) c. There is a unique solution, \( \mathbf{x}= \) D. There are infinitely many solutions of the form \( x=r x_{1}+s x_{2}+t x_{3} \), where \( r \), \( s \), and \( t \) are arbitrary parameters and \( \left\{x_{1}, x_{2}, x_{3}\right\}=\{ \) (Use a comma to separate vectors as needed.)