(Solved): Find the z-value that corresponds to each percentile for a standard normal distribution. a) 25th pe ...

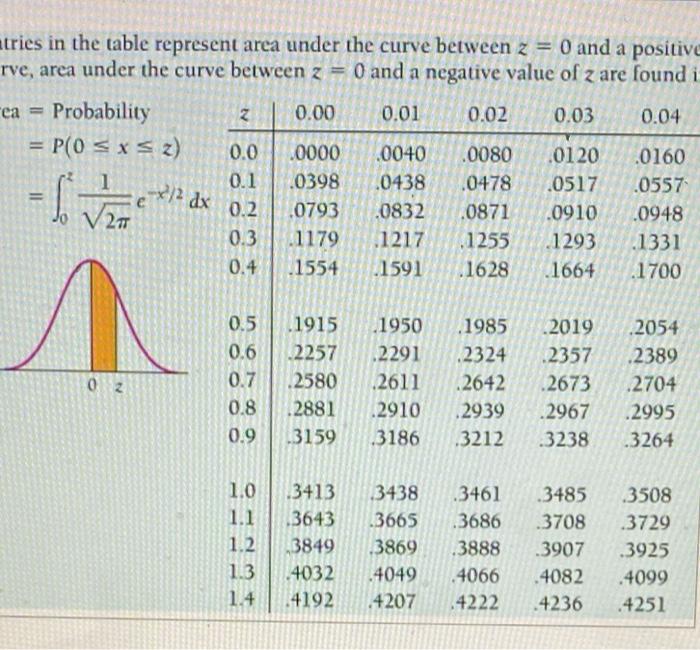
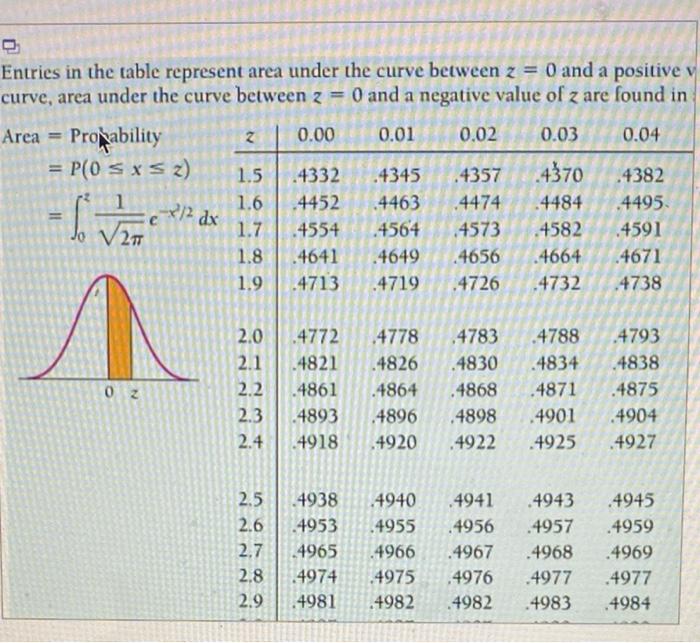
Find the z-value that corresponds to each percentile for a standard normal distribution. a) 25th percentile b) 50 th percentile c) 90 th percentile Click here to view page 1 of the standard normal distribution table. Click here to view page 2 of the standard normal distribution table. a) The z-value that corresponds to the 25 th percentile is b) The z-value that corresponds to the 50 th percentile is c) The z-value that corresponds to the 90th percentile is tries in the table represent area under the curve between \( z=0 \) and a positive rve, area under the cur \[ \begin{aligned} e a &=\text { Probability } \\ &=P(0 \leq x \leq z) \\ &=\int_{0}^{z} \frac{1}{\sqrt{2 \pi}} e^{-x^{2} / 2} d \end{aligned} \] Entries in the table represent area under the curve between \( z=0 \) and a nositive curve, area under the curv \[ \begin{aligned} \text { Area } &=\text { Pro } \frac{3 b i l i t y}{} \\ &=P(0 \leq x \leq z) \\ &=\int_{0}^{z} \frac{1}{\sqrt{2 \pi}} e^{-x^{2} / 2} d x \end{aligned} \]