(Solved): Find the number of elements in each of the following sets. \[ \begin{array}{l} U= \\ A^{C}= \\ A^{C ...

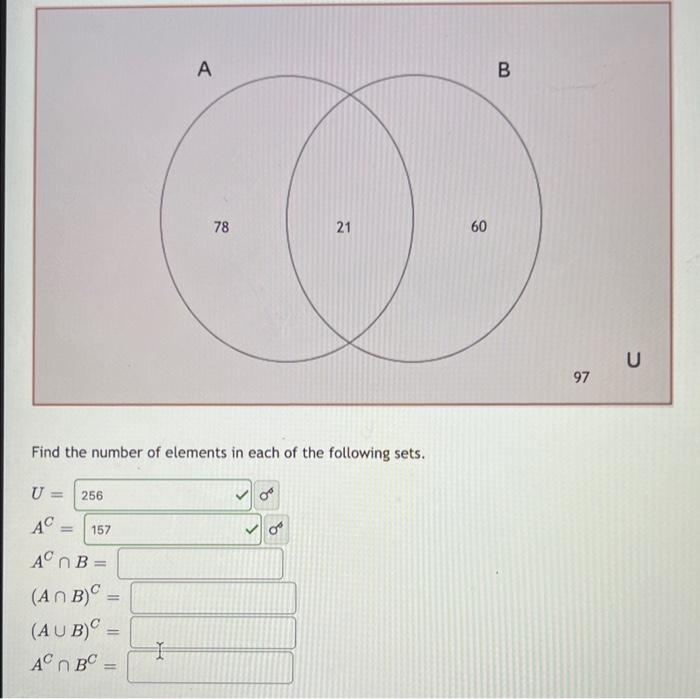
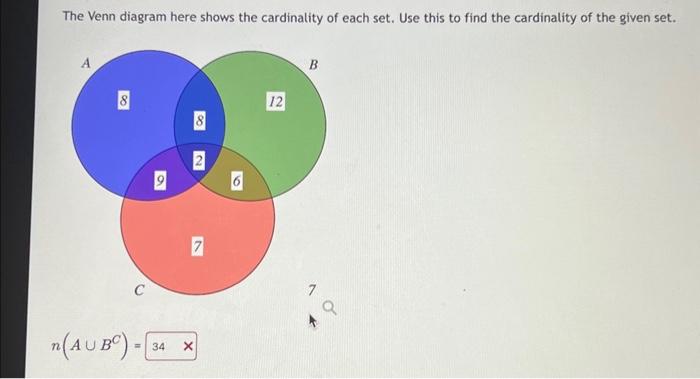
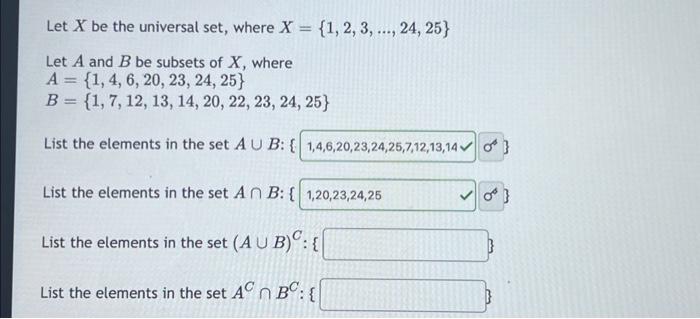
Find the number of elements in each of the following sets. \[ \begin{array}{l} U= \\ A^{C}= \\ A^{C} \cap B= \\ (A \cap B)^{C}= \\ (A \cup B)^{C}= \\ A^{C} \cap B^{C}= \end{array} \] The Venn diagram here shows the cardinality of each set. Use this to find the cardinality of the given set. \[ n\left(A \cup B^{C}\right)= \] Let \( X \) be the universal set, where \( X=\{1,2,3, \ldots, 24,25\} \) Let \( A \) and \( B \) be subsets of \( X \), where \[ \begin{array}{l} A=\{1,4,6,20,23,24,25\} \\ B=\{1,7,12,13,14,20,22,23,24,25\} \end{array} \] List the elements in the set \( A \cup B:\{ \) List the elements in the set \( A \cap B:\{ \) List the elements in the set \( (A \cup B)^{C}:\{ \) List the elements in the set \( A^{C} \cap B^{C}:\{ \) 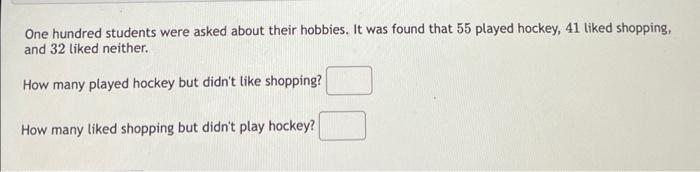One hundred students were asked about their hobbies. It was found that 55 played hockey, 41 liked shopping, and 32 liked neither. How many played hockey but didn't like shopping? How many liked shopping but didn't play hockey? Given \( n(U)=177, n(A)=84, n(B)=93 \), and \( n(A \cap B)=12 \), find a) \( n(A \cup B)= \) b) \( n\left(A^{C}\right)= \)