(Solved): Find the derivation of equation of motion and explain each equation in a clear way.     ...

Find the derivation of equation of motion and explain each equation in a clear way.

 

 

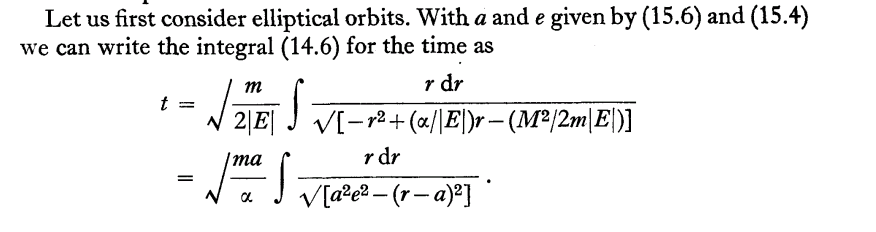
Now a days i can see experts simply copying the answers instead of solving properly in their own, in that scenario will be given more dislikes and will report. Solve it only if you are aware and know else skip it.

The shape of the path is obtained from the general formula (14.7). Sul tuting there \( U=-\alpha / r \) and effecting the elementary integration, we hat \[ \phi=\cos ^{-1} \frac{(M / r)-(m \alpha / M)}{\sqrt{\left(2 m E+\frac{m^{2} \alpha^{2}}{M^{2}}\right)}}+\text { constant. } \] Taking the origin of \( \phi \) such that the constant is zero, and putting \[ p=M^{2} / m \alpha, \quad e=\sqrt{ }\left[1+\left(2 E M^{2} / m \alpha^{2}\right)\right], \] we can write the equation of the path as \[ p / r=1+e \cos \phi \] Let us first consider elliptical orbits. With \( a \) and \( e \) given by (15.6) and (15.4) we can write the integral (14.6) for the time as \( t=\sqrt{\frac{m}{2|E|}} \int \frac{r \mathrm{~d} r}{\sqrt{\left[-r^{2}+(\alpha /|E|) r-\left(M^{2} / 2 m|E|\right)\right]}} \)