Home /
Expert Answers /
Advanced Math /
find-the-area-of-the-region-cut-from-the-plane-2-x-y-2-z-6-by-the-cylinder-whose-walls-are-pa388
(Solved): Find the area of the region cut from the plane \( 2 x+y+2 z=6 \) by the cylinder whose walls are \ ...
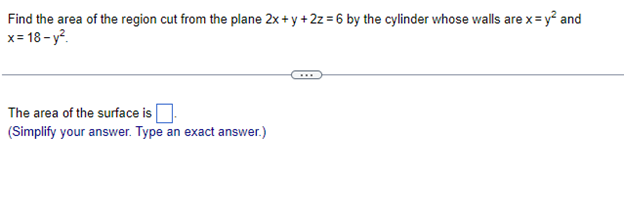
Find the area of the region cut from the plane \( 2 x+y+2 z=6 \) by the cylinder whose walls are \( x=y^{2} \) and \( \mathrm{x}=18-\mathrm{y}^{2} \) The area of the surface is (Simplify your answer. Type an exact answer.)
Expert Answer
We can write 2x+y+2z=6as z=6?2x?y2 Next, region bound