Home /
Expert Answers /
Calculus /
find-a-power-series-representation-for-the-function-determine-the-interval-of-convergence-give-y-pa139
(Solved): Find a power series representation for the function. Determine the interval of convergence. (Give y ...
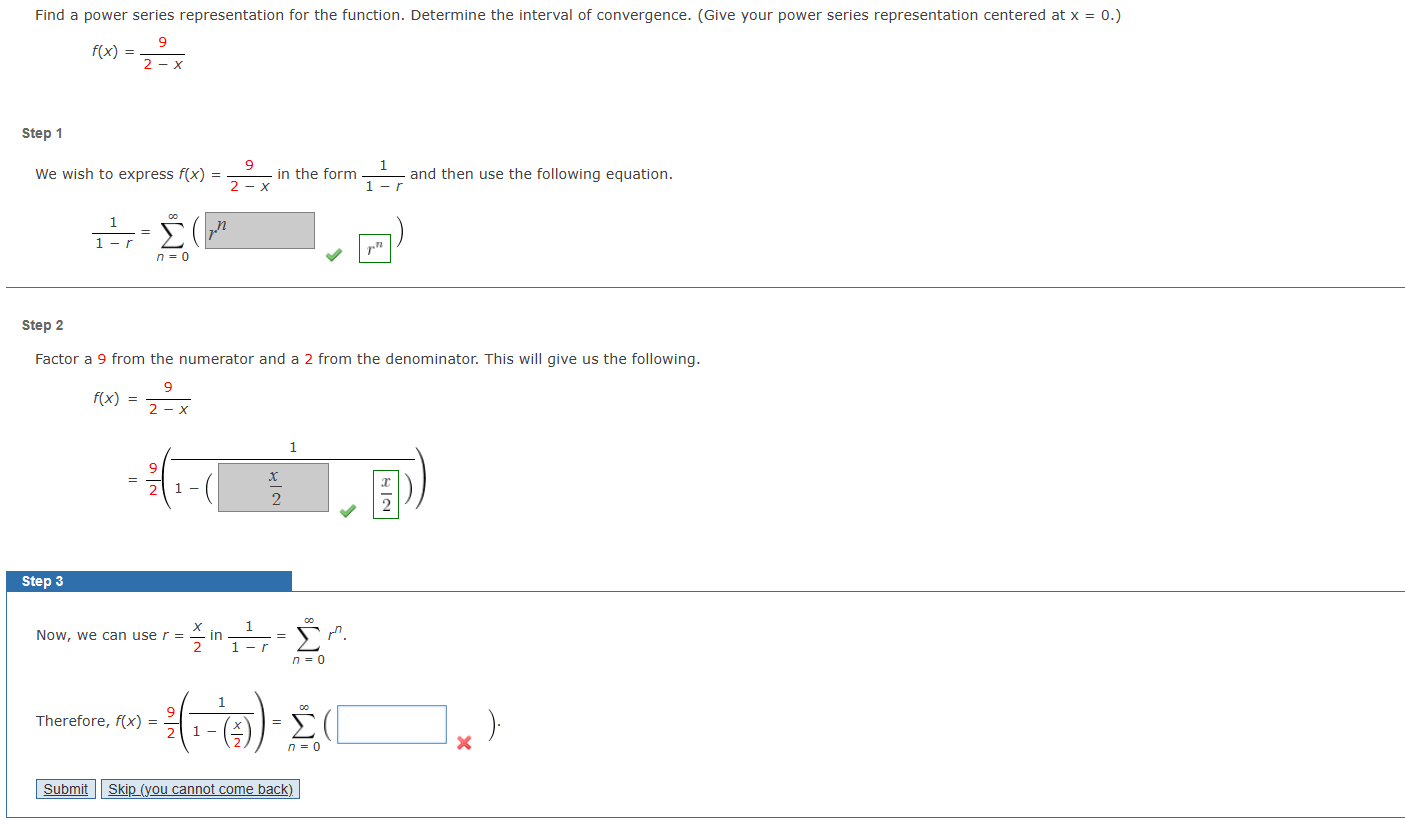
Find a power series representation for the function. Determine the interval of convergence. (Give your power series representation centered at
x=0.)
f(x)=(9)/(2-x)Step 1 We wish to express
f(x)=(9)/(2-x)in the form
(1)/(1-r)and then use the following equation.
(1)/(1-r)=\sum_(n=0)^(\infty ) (,r^(n))Step 2 Factor a 9 from the numerator and a 2 from the denominator. This will give us the following. Step 3 Now, we can use
r=(x)/(2)in
(1)/(1-r)=\sum_(n=0)^(\infty ) r^(n). Therefore,
f(x)=(9)/(2)((1)/(1-((x)/(2))))=\sum_(n=0)^(\infty ) (,x).