(Solved): Fill out the table below and use the totals to obtain the values of B1, B0 and R2. Use the formulas ...

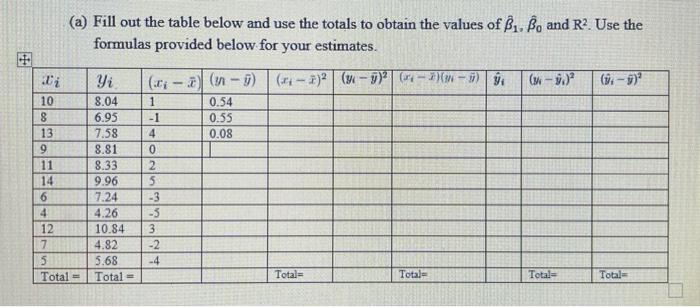
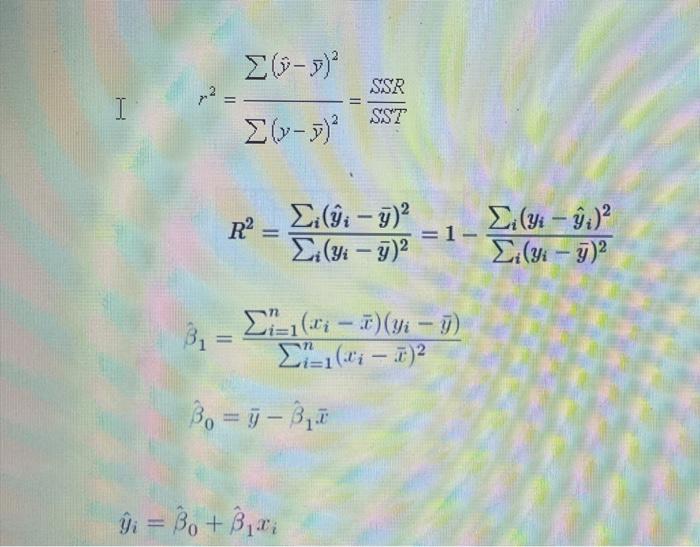
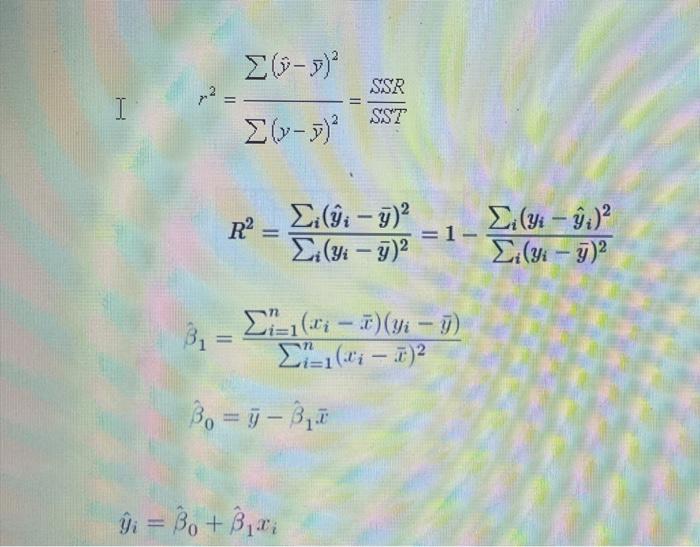
(a) Fill out the table below and use the totals to obtain the values of \( \hat{\beta}_{1}, \hat{\beta}_{0} \) and \( R^{2} \). Use the formulas provided below for your estimates. \( r^{2}=\frac{\sum(\hat{y}-\bar{y})^{2}}{\sum(y-\bar{y})^{2}}=\frac{S S R}{S S T} \) \( R^{2}=\frac{\sum_{i}\left(\hat{y}_{i}-\bar{y}\right)^{2}}{\sum_{i}\left(y_{i}-\bar{y}\right)^{2}}=1-\frac{\sum_{i}\left(y_{i}-\hat{y}_{i}\right)^{2}}{\sum_{i}\left(y_{i}-\bar{y}\right)^{2}} \) \( \hat{\beta}_{1}=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \) \( \hat{\beta}_{0}=\bar{y}-\hat{\beta}_{1} \bar{x} \)