(Solved): Exercise 2: Introduction to closed loop We will simulate responses for open loop and closed loop a ...

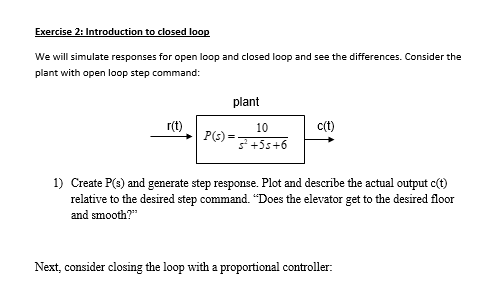
Exercise 2: Introduction to closed loop We will simulate responses for open loop and closed loop and see the differences. Consider the plant with open loop step command: 1) Create \( \mathrm{P}(\mathrm{s}) \) and generate step response. Plot and describe the actual output \( c(\mathrm{t}) \) relative to the desired step command. "Does the elevator get to the desired floor and smooth?" Next, consider closing the loop with a proportional controller: A transfer function can be described by the command tf with specifying the coefficients of the numerator and denominator. These type of tf variables then can be combined (add or multiply) algebraically. Furthermore, time response to a step input can be generated using the step command. Response to an arbitrary input can be generated using the Isim command. \( > \) clear \( >> \) num \( =[10] ; \quad \% \) this vector captures the numerator coefficients in descending order \( > \) sen \( =\left[\begin{array}{lll}1 & 3 & 1\end{array}\right] ; \quad \% \) this vector captures the denomerator coefficients in descending order \( >> \) help tf \( \quad \% \) read this about built-in command \( >>\mathrm{G}=\mathrm{tf}( \) num, den) \( \quad \% \) this constructs the transfer function \( \mathrm{G}(\mathrm{s}) \) \( >P=? \quad \) \% Do the same for \( P(s) \) >> help step \( \quad \) \% read help for the built-in command \( >>[c t]=\operatorname{step}(P, 6) ; \quad \) \% This generates a step response for \( P \), i.e. e(t)=step >> plot(t,c); \( >>L=G^{*} P ; \quad \) \% Open loop transfer function \( L=C / E=G(s)^{*} P(s) \) \( >>\quad \) \% display transfer function \( \mathrm{L} \)