(Solved): EXAMPLE 1 (a) As dry air moves upward, it expands and cools. If the ground temperature is \\( 25^{\ ...

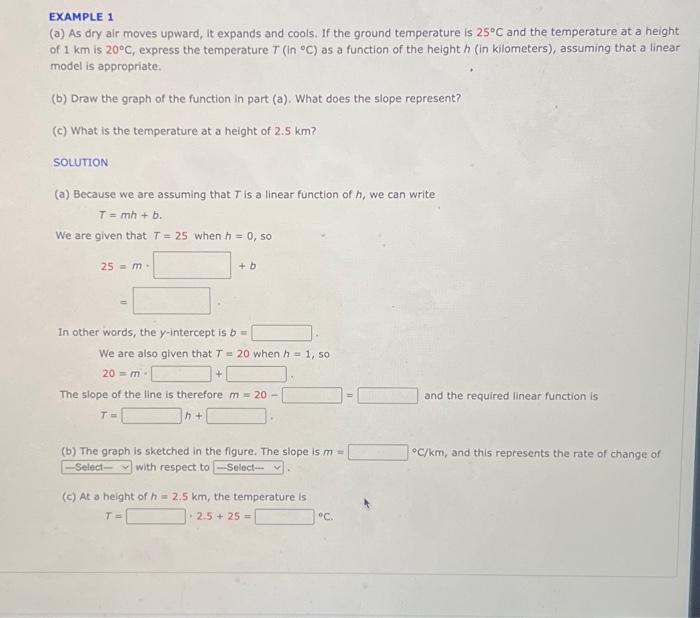
EXAMPLE 1 (a) As dry air moves upward, it expands and cools. If the ground temperature is \\( 25^{\\circ} \\mathrm{C} \\) and the temperature at a height of \\( 1 \\mathrm{~km} \\) is \\( 20^{\\circ} \\mathrm{C} \\), express the temperature \\( T\\left(i n{ }^{\\circ} \\mathrm{C}\\right. \\) ) as a function of the height \\( h \\) (in kilometers), assuming that a linear model is appropriate. (b) Draw the graph of the function in part (a). What does the slope represent? (c) What is the temperature at a height of \\( 2.5 \\mathrm{~km} \\) ? SOLUTION (a) Because we are assuming that \\( T \\) is a linear function of \\( h \\), we can write \\[ T=m h+b . \\] We are given that \\( T=25 \\) when \\( h=0 \\), so \\[ \\begin{aligned} 25 & =m \\cdot+b \\\\ & = \\end{aligned} \\] In other words, the \\( y \\)-intercept is \\( b= \\) We are also given that \\( T=20 \\) when \\( h=1 \\), so \\[ 20=m \\text {. } \\] The slope of the line is therefore \\( m=20- \\) \\[ T=h+ \\] (b) The graph is sketched in the figure. The slope is \\( m= \\) with respect to \\( { }^{\\circ} \\mathrm{C} / \\mathrm{km} \\), and this represents the rate of change of (c) At a height of \\( h=2.5 \\mathrm{~km} \\), the temperature is \\[ T=\\cdot 2.5+25= \\] \\( { }^{\\circ} \\mathrm{C} \\).