(Solved): Dixie Showtime Movie Theaters, Inc., owns and operates a chain of cinemas in several markets in the ...

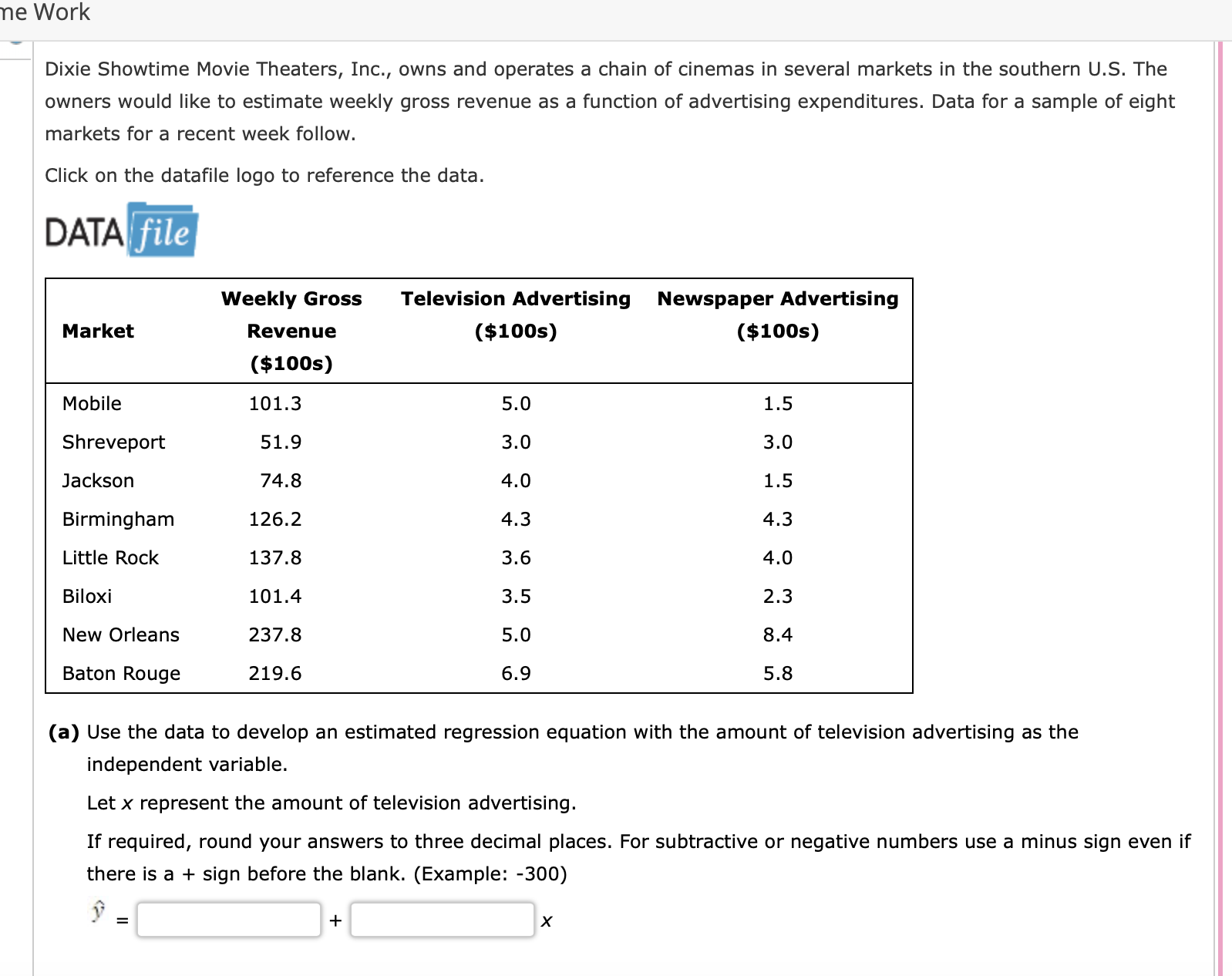
Dixie Showtime Movie Theaters, Inc., owns and operates a chain of cinemas in several markets in the southern U.S. The owners would like to estimate weekly gross revenue as a function of advertising expenditures. Data for a sample of eight markets for a recent week follow. Click on the datafile logo to reference the data. DATA (a) Use the data to develop an estimated regression equation with the amount of television advertising as the independent variable. Let $x$ represent the amount of television advertising. If required, round your answers to three decimal places. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300 ) $\hat{y}=?+x$ Test for a significant relationship between television advertising and weekly gross revenue at the 0.05 level of significance. What is the interpretation of this relationship? There a significant relationship between the amount spent on television advertising and weekly gross revenue. The estimated regression equation is the best estimate of the - Select your answer. given the b) How much of the variation in the sample values of weekly gross revenue does the model in part (a) explain? If required, round your answer to two decimal places. $\%$ c) Use the data to develop an estimated regression equation with both television advertising and newspaper advertising as the independent variables. Let $x_1$ represent the amount of television advertising. Let $x_2$ represent the amount of newspaper advertising. If required, round your answers to three decimal places. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. (Example: -300) $\hat{y}=?+?x_1+x_2$ Test whether each of the regression parameters ${?}_0,{?}_1$, and ${?}_2$ is equal to zero at a 0.05 level of significance. \begin{tabular}{ll} We 1 & conclude that ${?}_0=0$. \\ We & conclude that ${?}_1=0$. \\ We & conclude that ${?}_2=0$. \end{tabular} (i) ${?}_0$ is the estimate of the weekly gross revenue when television and newspaper advertising are both zero. ${?}_1$ is the estimate of change in the weekly gross revenue if newspaper advertising is held constant and there is a $\$100$ increase in television advertising. ${?}_2$ is the estimate of change in the weekly gross revenue if television advertising is held constant and there is a $\$100$ increase in newspaper advertising. The interpretation of ${?}_0$ is not reasonable but the interpretations of ${?}_1$ and ${?}_2$ are reasonable. (ii) ${?}_0$ is the estimate of the weekly gross revenue when television and newspaper advertising are both zero. ${?}_1$ is the estimate of change in the weekly gross revenue if television advertising is held constant and there is a $\$100$ increase in newspaper advertising. ${?}_2$ is the estimate of change in the weekly gross revenue if newspaper advertising is held constant and there is a $\$100$ increase in television advertising. The interpretation of ${?}_0$ is not reasonable but the interpretations of ${?}_1$ and ${?}_2$ are reasonable. (iii) ${?}_0$ is the estimate of change in the weekly gross revenue if newspaper advertising is held constant and there is a $\$100$ increase in television advertising. ${?}_1$ is the estimate of change in the weekly gross revenue if television advertising is held constant and there is a $\$100$ increase in newspaper advertising. ${?}_2$ is the estimate of the weekly gross revenue when television and newspaper advertising are both zero. The interpretation of ${?}_0,{?}_1$, and ${?}_2$ are all reasonable. d) How much of the variation in the sample values of weekly gross revenue does the model in part (c) explain? If required, round your answer to two decimal places. $\%$ e) Given the results in part (a) and part (c), what should your next step be? Explain. The input in the box below will not be graded, but may be reviewed and considered by your instructor.