(Solved): District Math Use the table of common logical equivalences below to verify the given logical equiv ...

District Math

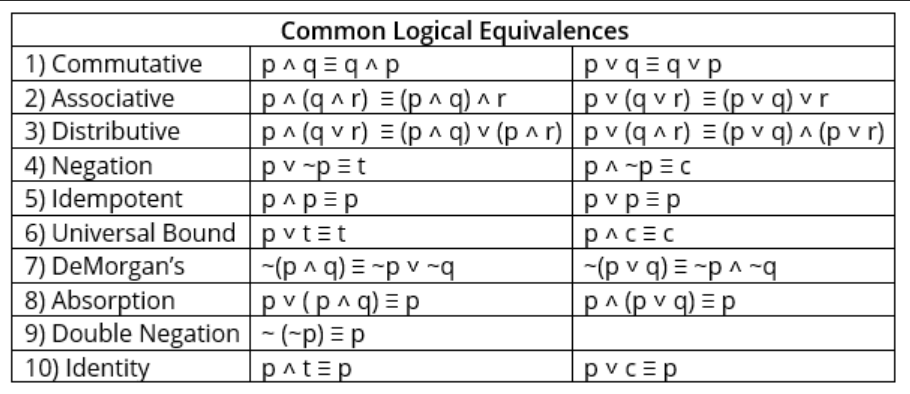
Use the table of common logical equivalences below to verify the given logical equivalence. Justify each step. Do not use a truth table. You will not receive credit. \[ \sim((\sim p \wedge q) \vee(\sim p \wedge \sim q)) \vee(p \wedge q) \equiv p \] \begin{tabular}{|l|l|l|} \hline \multicolumn{3}{|c|}{ Common Logical Equivalences } \\ \hline 1) Commutative & \( p \wedge q \equiv q \wedge p \) & \( p \vee q \equiv q \vee p \) \\ \hline 2) Associative & \( p \wedge(q \wedge r) \equiv(p \wedge q) \wedge r \) & \( p \vee(q \vee r) \equiv(p \vee q) \vee r \) \\ \hline 3) Distributive & \( p \wedge(q \vee r) \equiv(p \wedge q) \vee(p \wedge r) \) & \( p \vee(q \wedge r) \equiv(p \vee q) \wedge(p \vee r) \) \\ \hline 4) Negation & \( p \vee \sim p \equiv t \) & \( p \wedge \sim p \equiv c \) \\ \hline 5) Idempotent & \( p \wedge p \equiv p \) & \( p \vee p \equiv p \) \\ \hline 6) Universal Bound & \( p \vee t \equiv t \) & \( p \wedge c \equiv c \) \\ \hline 7) DeMorgan's & \( \sim(p \wedge q) \equiv \sim p \vee \sim q \) & \( \sim(p \vee q) \equiv \sim p \wedge \sim q \) \\ \hline 8) Absorption & \( p \vee(p \wedge q) \equiv p \) & \( p \wedge(p \vee q) \equiv p \) \\ \hline 9) Double Negation & \( \sim(\sim p) \equiv p \) & \\ \hline 10) Identity & \( p \wedge t \equiv p \) & \( p \vee c \equiv p \) \\ \hline \end{tabular}