Home /
Expert Answers /
Advanced Math /
determine-whether-the-following-lines-in-r2-represented-by-the-vector-equations-below-intersect-ar-pa482
(Solved): Determine whether the following lines in R2 represented by the vector equations below intersect, ar ...
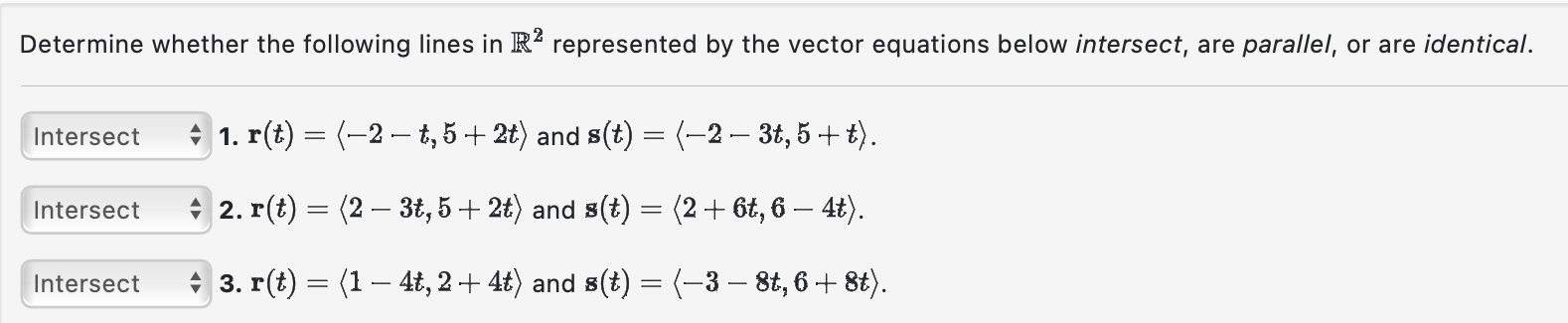
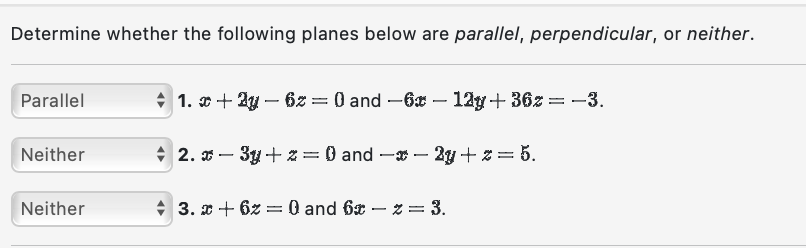
Determine whether the following lines in represented by the vector equations below intersect, are parallel, or are identical. 1. and . 2. and . 3. and .
Determine whether the following planes below are parallel, perpendicular, or neither. 1. and . 2. and . 3. and .
Expert Answer
There are two questions each containing 3 parts now first we solve 1 st question:- Apologies for the errors in the previous response. Let's reanalyze the given vector equations. The direction vector of line r is ?-1, 2?, and the direction vector of line s is ?-3, 1?. The direction vectors are not scalar multiples of each other, so the lines are not parallel.To check if they intersect, we set the x-components and y-components equal to each other and solve for t:-2 - t = -2 - 3t => 2t = 0 => t = 05 + 2t = 5 + t => 2t = t => t = 0The values of t are the same for both equations, indicating that the lines intersect at the point (-2, 5) when t = 0. Therefore, the lines intersect.2 . The direction vector of line r is ?-3, 2?, and the direction vector of line s is ?6, -4?. The direction vectors are not scalar multiples of each other, so the lines are not parallel.To check if they intersect, we set the x-components and y-components equal to each other and solve for t:2 - 3t = 2 + 6t => -9t = 0 => t = 05 + 2t = 6 - 4t => 6t = 1 => t = 1/6The values of t are different for both equations, indicating that the lines do not intersect. Therefore, the lines are parallel.