(Solved): Determine the output voltage in the phasor domain of an LC circuit. Given: \( X_{L}=15 \mathrm{k} \ ...

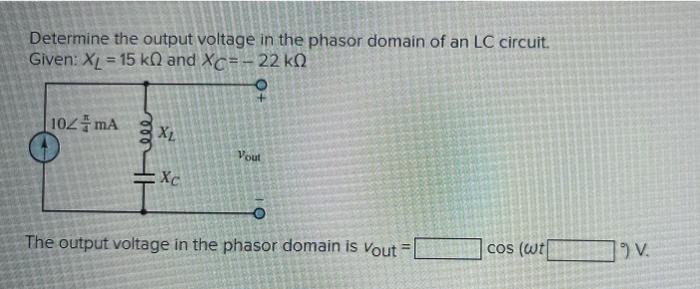
Determine the output voltage in the phasor domain of an LC circuit. Given: \( X_{L}=15 \mathrm{k} \Omega \) and \( X_{C}=-22 \mathrm{k} \Omega \) The output voltage in the phasor domain is \( v_{\text {out }}= \) \( \cos (\omega t) \) A common model fot a practical inductor is a coll resistance in series with an inductance \( L \) The coll resistance accounts for the internal losses of an inductor. The circult shows an ideal capacitor in parallel with a practical inductor. Determine the current supplied by the source \( v_{S} \) Assume \( v_{s}(0)=V_{0} \cos (\omega t+0), V_{0}=10 \mathrm{~V}, L=39 \mu H, R_{S}=54.75 \Omega, R_{C}=43.8 \Omega, \omega=6 \mathrm{M} \frac{\mathrm{nmi}}{\mathrm{I}} \), and \( C=1.25 \mathrm{nF} \). The current supplied by the source is is \( (t)= \) \( \cos (\omega t- \) 9 \( \mathrm{mA} \)