(Solved): Determine the height that water at \( 60^{\circ} \mathrm{F} \) will rise due to capillary action in ...

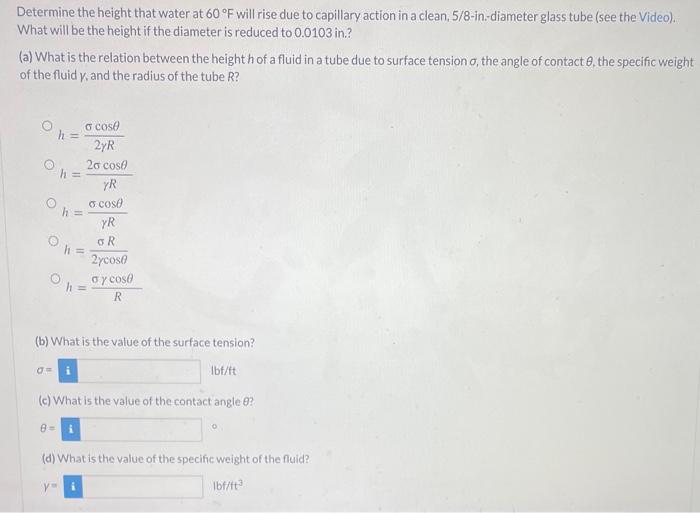
Determine the height that water at \( 60^{\circ} \mathrm{F} \) will rise due to capillary action in a clean, \( 5 / 8 \)-in.-diameter glass tube (see the Video). What will be the height if the diameter is reduced to \( 0.0103 \) in.? (a) What is the relation between the height h of a fluid in a tube due to surface tension \( \sigma \), the angle of contact \( \theta \), the specific weight of the fluid \( \gamma \), and the radius of the tube R? \[ \begin{aligned} h &=\frac{\sigma \cos \theta}{2 \gamma R} \\ h &=\frac{2 \sigma \cos \theta}{\gamma R} \\ h &=\frac{\sigma \cos \theta}{\gamma R} \\ h &=\frac{\sigma R}{2 \gamma \cos \theta} \\ h &=\frac{\sigma \gamma \cos \theta}{R} \end{aligned} \] (b) What is the value of the surface tension? \[ \sigma= \] lbf/it (c) What is the value of the contact angle \( \theta \) ? \[ \theta= \] (d) What is the value of the specific weight of the fluid? \[ y= \] \( 1 \mathrm{bf} / \mathrm{tt}^{3} \) What is the height that the water will rise in the tube? \[ h= \] in. eTextbook and Media Part 3 For the small diameter tube, what is the height of the water? \[ h= \] in.