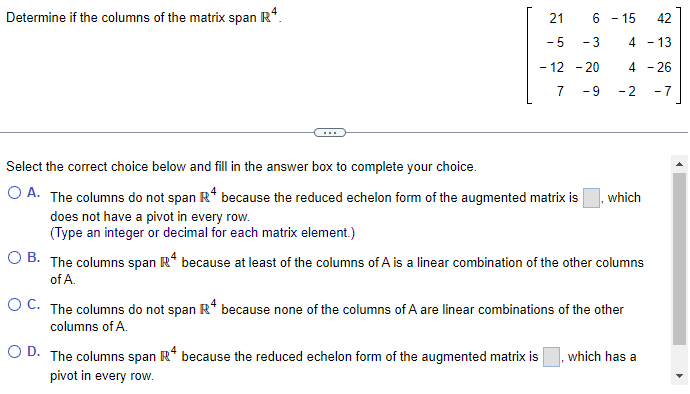
(Solved): Determine if the columns of the matrix span \( \mathbb{R}^{4} \) \[ \left[\begin{array}{rrrr} 21 & ...

Determine if the columns of the matrix span \( \mathbb{R}^{4} \) \[ \left[\begin{array}{rrrr} 21 & 6 & -15 & 42 \\ -5 & -3 & 4 & -13 \\ -12 & -20 & 4 & -26 \\ 7 & -9 & -2 & -7 \end{array}\right] \] Select the correct choice below and fill in the answer box to complete your choice. A. The columns do not span \( \mathrm{R}^{4} \) because the reduced echelon form of the augmented matrix is which does not have a pivot in every row. (Type an integer or decimal for each matrix element.) B. The columns span \( \mathbb{R}^{4} \) because at least of the columns of \( \mathrm{A} \) is a linear combination of the other columns of \( \mathrm{A} \). C. The columns do not span \( \mathbb{R}^{4} \) because none of the columns of \( A \) are linear combinations of the other columns of \( \mathrm{A} \). D. The columns span \( \mathbb{R}^{4} \) because the reduced echelon form of the augmented matrix is which has a pivot in every row.