(Solved): Determine if \( b \) is a linear combination of the vectors formed from the columns of the matrix ...

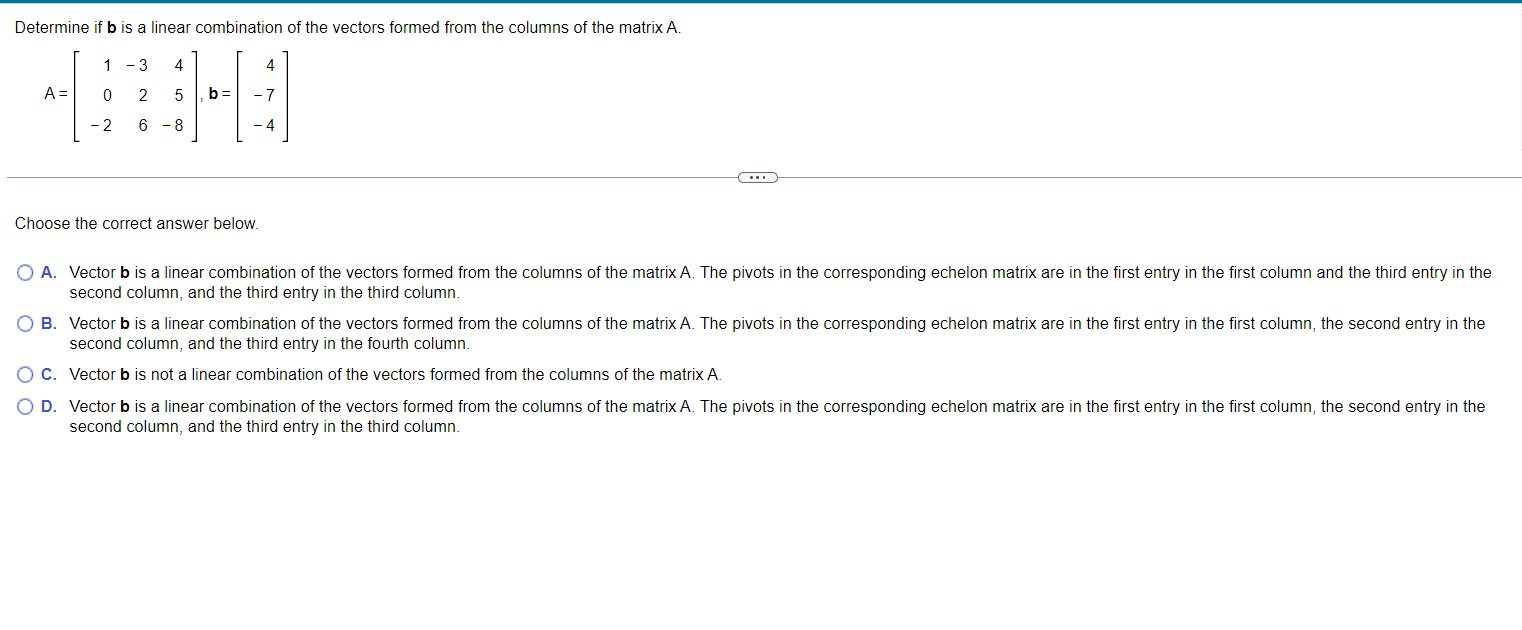
Determine if \( b \) is a linear combination of the vectors formed from the columns of the matrix \( \mathrm{A} \). \[ A=\left[\begin{array}{rrr} 1 & -3 & 4 \\ 0 & 2 & 5 \\ -2 & 6 & -8 \end{array}\right], \mathbf{b}=\left[\begin{array}{r} 4 \\ -7 \\ -4 \end{array}\right] \] Choose the correct answer below. A. Vector \( \mathbf{b} \) is a linear combination of the vectors formed from the columns of the matrix \( \mathrm{A} \). The pivots in the corresponding echelon matrix are in the first entry in the first column and the third entry in the second column, and the third entry in the third column. B. Vector \( \mathbf{b} \) is a linear combination of the vectors formed from the columns of the matrix A. The pivots in the corresponding echelon matrix are in the first entry in the first column, the second entry in the second column, and the third entry in the fourth column. C. Vector \( \mathbf{b} \) is not a linear combination of the vectors formed from the columns of the matrix \( \mathbf{A} \). D. Vector \( \mathbf{b} \) is a linear combination of the vectors formed from the columns of the matrix A. The pivots in the corresponding echelon matrix are in the first entry in the first column, the second entry in the second column, and the third entry in the third column.