(Solved): Consider the two-degree-of-freedom system shown in Figure 4 below: Assuming small-angle oscillation ...

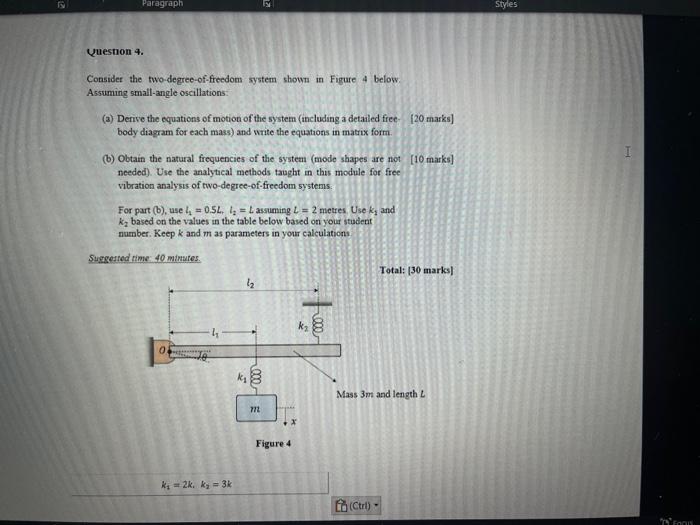
Consider the two-degree-of-freedom system shown in Figure 4 below: Assuming small-angle oscillations: (a) Derive the equations of motion of the system (including a detailed free- [20 marks] body diagram for each mass) and write the equations in matrix form. (b) Obtain the natural frequencies of the system (mode shapes are not [10 marks] needed). Use the analytical methods taught in this module for free vibration analysis of two-degree-of-freedom systems: For part (b), use \( L_{1}=0.5 L \), \( l_{2}=L \) assuming \( L=2 \) metres, Use \( k_{1} \) and \( k_{2} \) based on the values in the table below based on your itudent number. Keep \( k \) and \( m \) as parameters in your calculation. Suggestod rime 40 mintites. \[ k_{1}=2 k_{1} \quad k_{2}=3 k \]