(Solved): Consider the series \\[ \\sum_{n=1}^{\\infty} \\frac{33^{n}(n !)^{3}}{(3 n) !} \\] Let \\( a_{n}=\\ ...

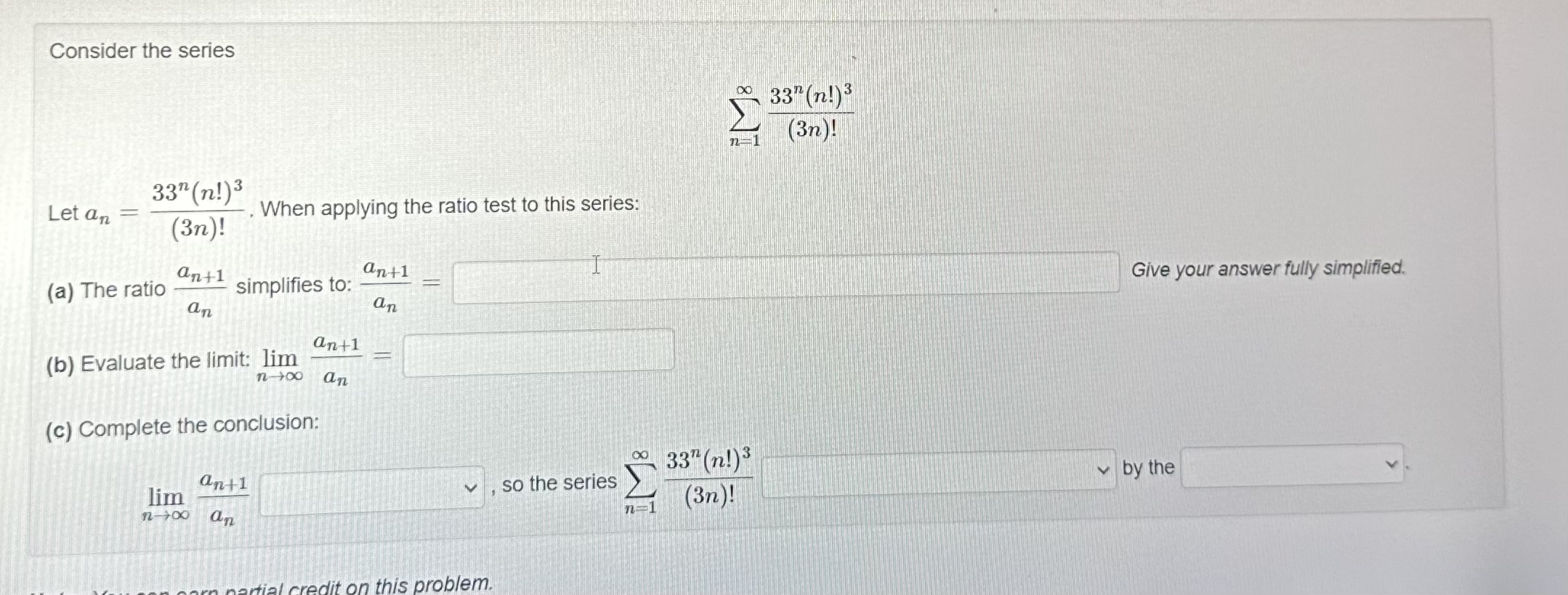
Consider the series \\[ \\sum_{n=1}^{\\infty} \\frac{33^{n}(n !)^{3}}{(3 n) !} \\] Let \\( a_{n}=\\frac{33^{n}(n !)^{3}}{(3 n) !} \\). When applying the ratio test to this series: (a) The ratio \\( \\frac{a_{n+1}}{a_{n}} \\) simplifies to: \\( \\frac{a_{n+1}}{a_{n}}= \\) Give your answer fully simplified. (b) Evaluate the limit: \\( \\lim _{n \\rightarrow \\infty} \\frac{a_{n+1}}{a_{n}}= \\) (c) Complete the conclusion: \\( \\lim _{n \\rightarrow \\infty} \\frac{a_{n+1}}{a_{n}} \\) so the series \\( \\sum_{n=1}^{\\infty} \\frac{33^{n}(n !)^{3}}{(3 n) !} \\) by the