Home /
Expert Answers /
Mechanical Engineering /
consider-the-sampled-data-system-shown-in-figure-2-1-in-figure-2-1-we-include-the-following-trans-pa983
(Solved): Consider the sampled-data system shown in Figure 2.1, In Figure 2.1, we include the following trans ...
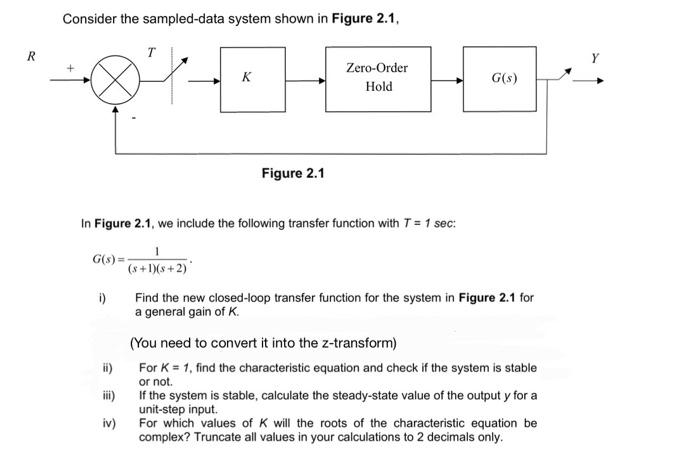
Consider the sampled-data system shown in Figure 2.1, In Figure 2.1, we include the following transfer function with sec: i) Find the new closed-loop transfer function for the system in Figure 2.1 for a general gain of . (You need to convert it into the -transform) ii) For , find the characteristic equation and check if the system is stable or not. iii) If the system is stable, calculate the steady-state value of the output for a unit-step input. iv) For which values of will the roots of the characteristic equation be complex? Truncate all values in your calculations to 2 decimals only.
Expert Answer
SolutionTo find the new closed-loop transfer function for the system in Figure 2.1, we can use the following steps:i) Convert the continuous-time transfer function into the discrete-time transfer function using the z-transform.The continuous-time transfer function, G(s), is given as: To convert it into the z-transform, we can use the bilinear transform method. Let's denote the discrete-time transfer function as G(z).The bilinear transform is defined as: Substituting the bilinear transform into G(s), we get: Substituting the given transfer function G(s), we have: ii) For K = 1, let's find the characteristic equation and check the stability of the system.The characteristic equation is obtained by setting the denominator of the closed-loop transfer function equal to zero.For K = 1, the closed-loop transfer function becomes: please refer the next step to the complete solutioon