Home /
Expert Answers /
Calculus /
consider-the-function-f-x-y-x-2-2-a-x-y-y-2-where-a-in-mathbb-r-a-i-find-al-pa251
(Solved): Consider the function \( f(x, y)=x^{2}+2 a x y+y^{2} \), where \( a \in \mathbb{R} \). (a)i find al ...
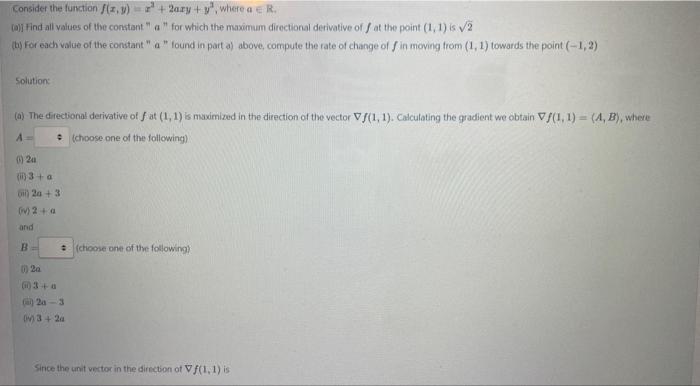
![Since the unit wector in the direction of \( V f(1,1) \) is
\[
\vec{u}=\frac{\nabla f(1,1)}{|\nabla f(1,1)|^{\prime}}
\]
for](https://media.cheggcdn.com/study/a3f/a3f548dc-05fb-4002-9ecd-c38483f7aff7/image)
Consider the function \( f(x, y)=x^{2}+2 a x y+y^{2} \), where \( a \in \mathbb{R} \). (a)i find all values of the constant " \( a \) " for which the maximum directional derivative of \( f \) at the point \( (1,1) \) is \( \sqrt{2} \) (b) for each value of the constant "a " found in part a) above, compute the rate of change of \( f \) in moving from \( (1,1) \) towards the point \( (-1,2) \) Solution: (a) The diectional derivative of \( f \) at \( (1,1) \) is maximized in the direction of the vector \( \nabla f(1,1) \). Calculating the gradient we obtain \( \nabla f(1,1)=(A, B) \), where A (choose one of the following) \( 2 a \) \( 3+a \) \( 2 a+3 \) (W) \( 2+a \) and (choose one of the following) \( 2 a \) \( 3+a \) \( 2 a-3 \) \( 3+2 a \) Sirice the unit vertor in the direction of \( \nabla f(1,1) \) is
Since the unit wector in the direction of \( V f(1,1) \) is \[ \vec{u}=\frac{\nabla f(1,1)}{|\nabla f(1,1)|^{\prime}} \] for the maximum directional derivative of \( f \) at \( (1,1) \) we get \[ D_{\bar{u}} f(1,1)=\nabla f(1,1) \cdot \vec{u}=|\nabla f(1,1)|=\sqrt{2(2 a+3)^{2}}=\sqrt{2}|2 a+3| \text {. } \] Hence, we have \[ D_{-} f(1,1)=\sqrt{2} \Rightarrow|2 a+3|=1 \Rightarrow a= \] (b) Let \( P \) denotes the point \( (1,1) \) and \( Q \) denotes the point \( (-1,-2) \). Then, the unit vector in the direction of \( \overrightarrow{P Q} \) is the victor Then \[ D_{*} f(1,1)=\nabla f(1,1) \cdot \vec{u}=\frac{1}{\sqrt{13}} \] Tor \( a=-2 \) we get \( D_{i} f(1,1)=\frac{1}{\sqrt{13}} \quad \) and for \( a=-1 \) we get \( D_{-} f(1,1)=\frac{1}{\sqrt{13}} \)