(Solved): Consider the following problem: a farmer with 750 feet of fencing wants to enclose a rectangular a ...

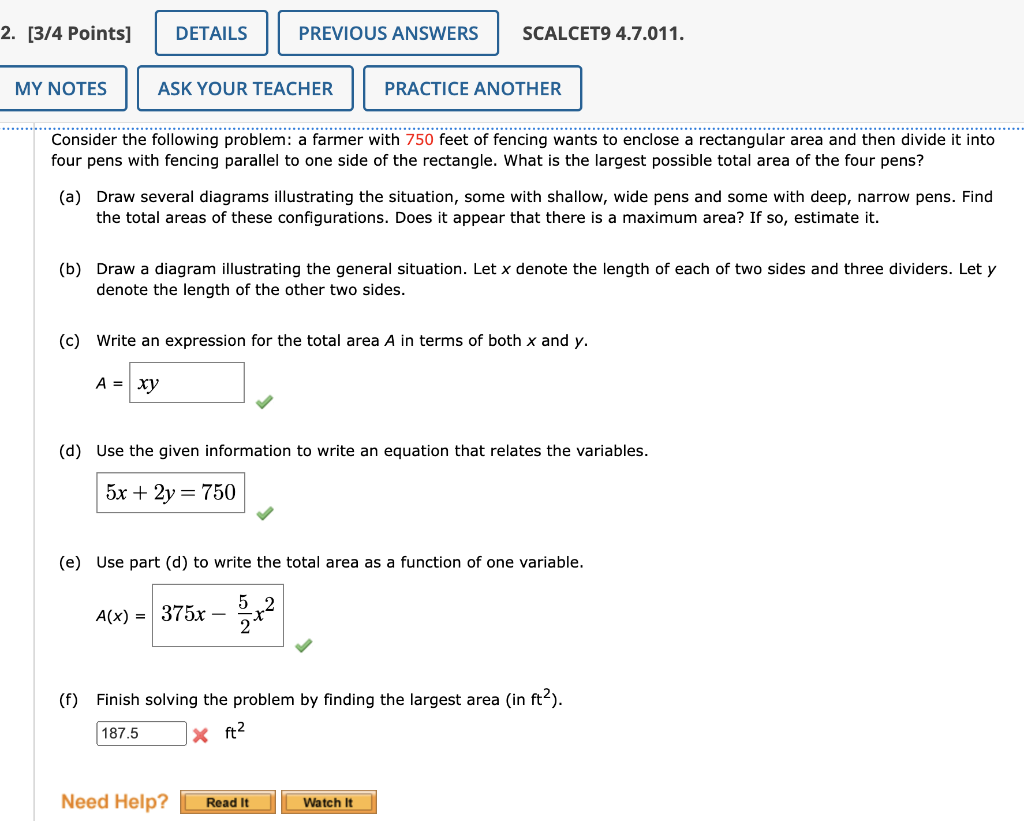
Consider the following problem: a farmer with 750 feet of fencing wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle. What is the largest possible total area of the four pens? (a) Draw several diagrams illustrating the situation, some with shallow, wide pens and some with deep, narrow pens. Find the total areas of these configurations. Does it appear that there is a maximum area? If so, estimate it. (b) Draw a diagram illustrating the general situation. Let \( x \) denote the length of each of two sides and three dividers. Let \( y \) denote the length of the other two sides. (c) Write an expression for the total area \( A \) in terms of both \( x \) and \( y \). \( A= \) (d) Use the given information to write an equation that relates the variables. \[ 5 x+2 y=750 \] (e) Use part (d) to write the total area as a function of one variable. \[ A(x)= \] (f) Finish solving the problem by finding the largest area (in \( \mathrm{ft}^{2} \) ). \[ \& \mathrm{ft}^{2} \]