(Solved): Consider the complex number \( z \) given below in rectangular form, and marked on the complex coor ...

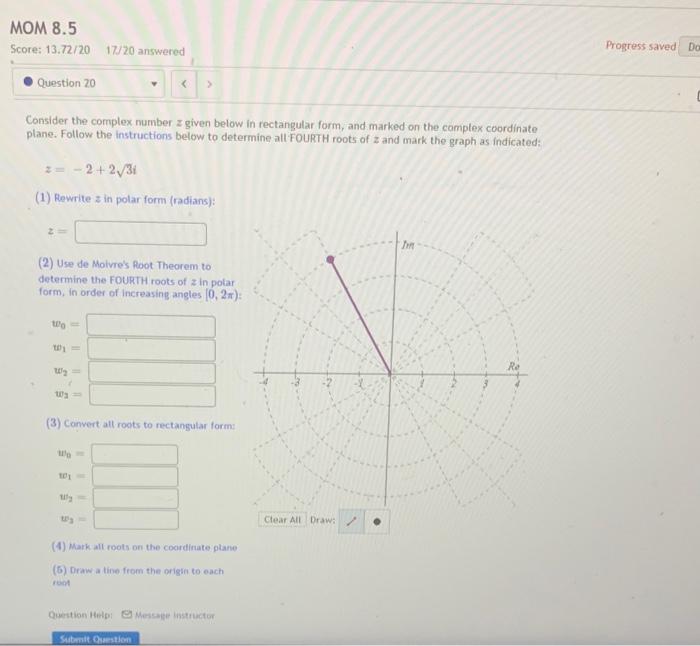
Consider the complex number \( z \) given below in rectangular form, and marked on the complex coordinate plane. Follow the instructions below to determine all FOURTH roots of \( z \) and mark the graph as indicated: \[ z=-2+2 \sqrt{3} i \] (1) Rewrite \( z \) in polar form (radians): \[ z= \] (2) Use de Moivre's poot Theorem to determine the FoURTH roots of \( z \) in polar form, in order of increasing angles \( (0,2 \pi) \) : \[ \begin{array}{l} w_{0}= \\ w_{1}= \\ w_{2}= \\ w_{2}= \end{array} \] (3) Convert all roots to rectangular form: (4) Mark all roots on the coordinate plane (5) Draw a tine from the origin to each