(Solved): Consider an irreversible chemical reaction process where component \( \mathrm{A} \) is decompose ...

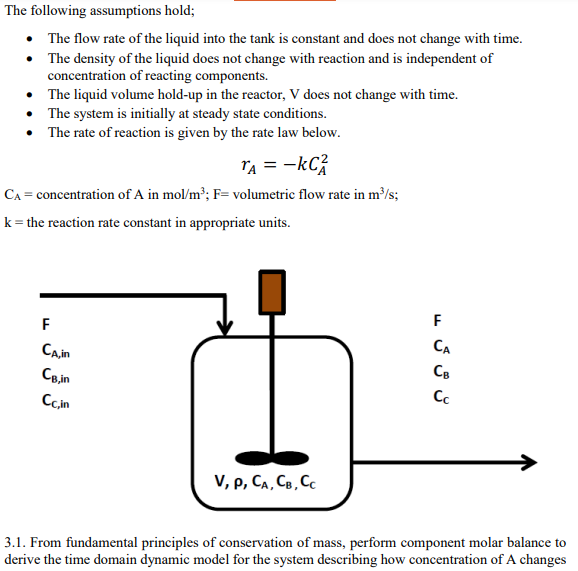
Consider an irreversible chemical reaction process where component \( \mathrm{A} \) is decomposed to form component \( \mathrm{C} \) through an instantaneous formation and decomposition of an intermediate component \( \mathrm{B} \) as shown in reaction below; A \( \quad \Rightarrow \quad \) B \( \quad \Rightarrow \quad \) C The reaction takes place in a perfectly mixed liquid in a continuous stirred tank reactor (CSTR). The following assumptions hold; - The flow rate of the liquid into the tank is constant and does not change with time. - The density of the liquid does not change with reaction and is independent of concentration of reacting components. - The liquid volume hold-up in the reactor, V does not change with time. - The system is initially at steady state conditions. - The rate of reaction is given by the rate law below. \[ r_{A}=-k C_{A}^{2} \] \( \mathrm{C}_{\mathrm{A}}= \) concentration of \( \mathrm{A} \) in \( \mathrm{mol} / \mathrm{m}^{3} ; \mathrm{F}= \) volumetric flow rate in \( \mathrm{m}^{3} / \mathrm{s} \) \( \mathrm{k}= \) the reaction rate constant in appropriate units. 3.1. From fundamental principles of conservation of mass, perform component molar balance to derive the time domain dynamic model for the system describing how concentration of \( \mathrm{A} \) changes 3.1. From fundamental principles of conservation of mass, perform component molar balance to derive the time domain dynamic model for the system describing how concentration of A changes with time. [7] 3.2. From the ODE you obtained in 3.1, derive the transfer function model to relate the output to input variables in their deviation states. The final equation should be in standard form. [23] Hint: Concentration of \( B \) is negligible since it instantaneously decomposes to form \( C \).