(Solved): can you help revised this python code to solve this problem using dynamic programming? I got di ...

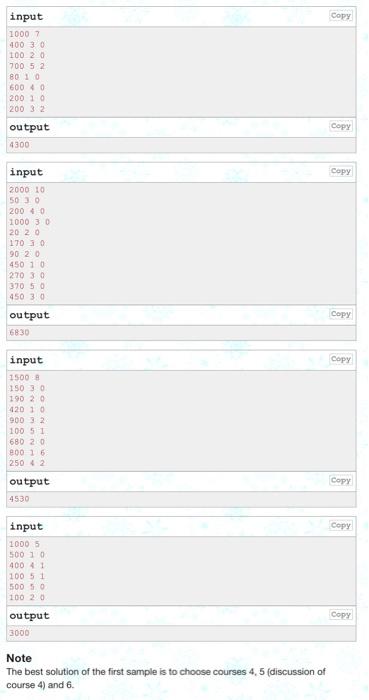
memory limit per test: 256 megabytes input: standard input output: standard output To further enthance your programming skills, you enrolled in an online CS program from UCR. In the program, you can enroll in whichever courses you want, and pay your tuition just for the courses you enroll in. The price for each course is different. We use \( p_{i} \) to denote the price of course \( i \). There are two different types of courses, main courses, and discussion courses. The discussion courses are always associated with exactly one main course. \( \mathrm{A} \) main course can have 0,1 , or 2 discussions. If you want to register for a discussion course, you have to register for its main course at the same time. However, if you want to register for a main course, you may choose to attend each of its discussions or not (either way is fine). For example, If you enroll in a course with two discussions. you can choose to enroll in neither discussions, or any one of them, or both of them. Before you choose the courses, you looked at the reviews of the courses online. Each of the courses has a rating \( r_{i} \) between 1 to 5 stars. 5 stars is the highest, Combining the price and rating, the yalue of each course is the product of rating and price \( \left(r_{i} \times p_{i}\right. \) for course \( \left.i\right) \). Your budget for taking this online program is \( m \) dollars. You want to know, based on the rules above, what is the highest total value \( \left(r_{i} \times p_{i}\right) \) you can get from the courses you enroll in. Input The first line contains two integers, \( m(1 \leq m \leq 32000) \), which is the budget, and \( n(1 \leq n \leq 60) \). which is the number of courses available. The next \( n \) lines each contains three integers \( p_{i}, r_{i}, c_{i}(1 \leq i \leq n) \), describing a course. \( p_{i} \) is the price of this course, \( r_{i} \) is the rating of the course. \( c_{i} \) describes if this course is a main course or discussion. If \( c_{i}=0 \), this course is a main course. If \( c_{i}=1 \), this course is a discussion, and its main course is course \( c_{i} \). The labels of the courses start from 1. Output There is only one integer in the output, which is the highest value you can get. The output is guaranteed to be within \( 2 \times 10^{5} \). def solve \( (m, n \), courses): \( d p=[[0] *(m+1) \) for \( - \) in range \( (n+1)] \) for \( i \) in range \( (1, n+1) \) : \( \quad p, r, c= \) courses \( [i-1] \) for \( j \) in range \( (1, m+1) \) : \( \quad \) if \( c=0 \) : \( \quad d p[i][j]=\max (d p[i-1][j], d p[i-1][j-p]+r * p) \) \( \quad \) else: \( \quad d p[i][j]=\max (d p[i-1][j], d p[i-1][j-p]+r * p, d p[c-1][j-p]+r * p) \) return \( d p[n][m] \) Note The best solution of the first sample is to choose courses 4,5 (discussion of course 4) and 6.