(Solved): Can someone help with this program in python There is another version of Euclid's algorithm kn ...

Can someone help with this program in python

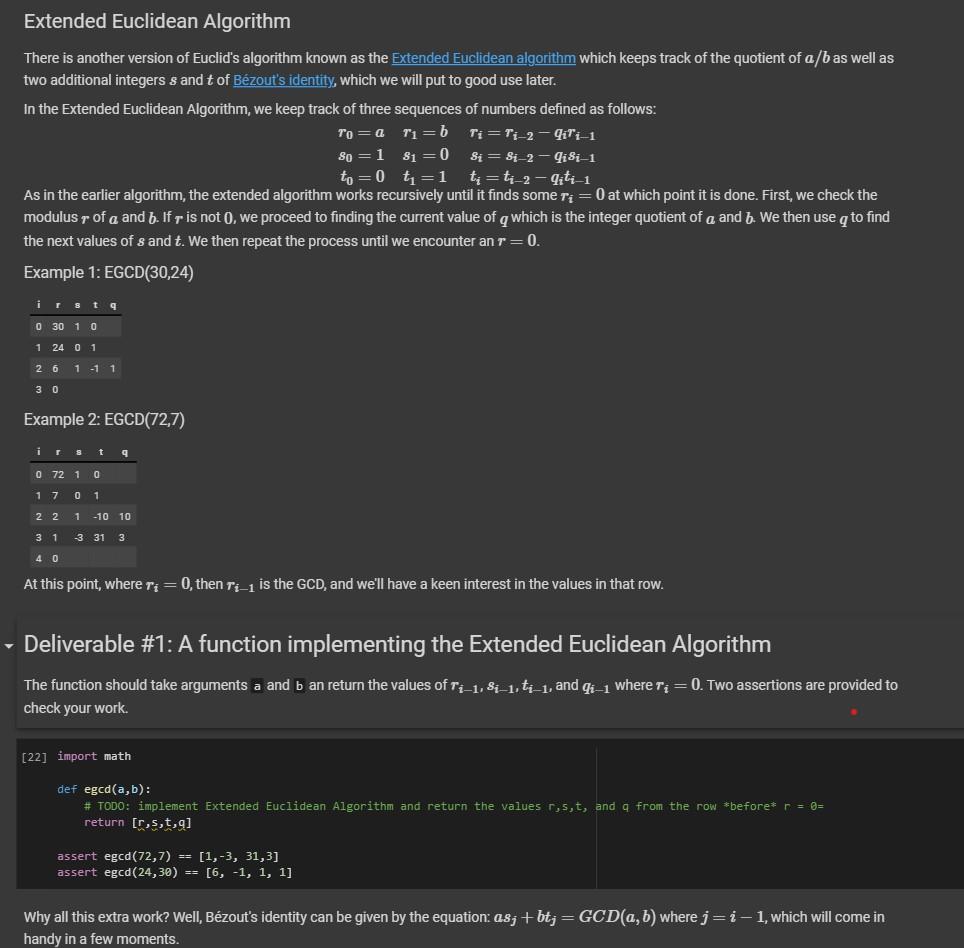
There is another version of Euclid's algorithm known as the Extended Euclidean algorithm which keeps track of the quotient of $$a/b$$ as well as two additional integers $$s$$ and $$t$$ of Bézout's identity, which we will put to good use later. In the Extended Euclidean Algorithm, we keep track of three sequences of numbers defined as follows: $$\begin{array}{rll}{r}_0=a& r_1=b& r_i=r_{i?2}?q_i{r}_{i?1}\\ s_0=1& s_1=0& s_i=s_{i?2}?q_i{s}_{i?1}\\ t_0=0& t_1=1& t_i=t_{i?2}?q_i{t}_{i?1}\end{array}$$ As in the earlier algorithm, the extended algorithm works recursively until it finds some $$r_i=0$$ at which point it is done. First, we check the modulus $$\mathbf{r}$$ of $$a$$ and $$b$$. If $$\mathbf{r}$$ is not $$0$$, we proceed to finding the current value of $$q$$ which is the integer quotient of $$a$$ and $$b$$. We then use $$q$$ to find the next values of $$s$$ and $$t$$. We then repeat the process until we encounter an $$\mathbf{r}=0$$. Example 1: $$\mathrm{EGCD}(30,24)$$ Example 2: $$\mathrm{EGCD}(72,7)$$ At this point, where $$r_i=0$$, then $$r_{i?1}$$ is the $$\mathrm{GCD}$$, and we'll have a keen interest in the values in that row. Deliverable \#1: A function implementing the Extended Euclidean Algorithm The function should take arguments $$\mathrm{a}$$ and $$\mathrm{b}$$ an return the values of $$r_{i?1},s_{i?1},t_{i?1}$$, and $$q_{i?1}$$ where $$r_i=0$$. Two assertions are provided to check your work. [22] import math def egcd $$(a,b)$$ : \# TODO: implement Extended Euclidean Algorithm and return the values r, $$5,t$$, and $$q$$ from the row $$?$$ before* $$r=0=$$ return $$[r,5,t,q]$$ assert $$\mathrm{egcd}(72,7)=[1,?3,31,3]$$ assert $$\mathrm{egcd}(24,30)=[6,?1,1,1]$$ Why all this extra work? Well, Bézout's identity can be given by the equation: $$a{s}_j+b{t}_j=GCD(a,b)$$ where $$j=i?1$$, which will come in handy in a few moments.