(Solved): At the bottom of a loop in the vertical plane, an airplane has a horizontal velocity of \( 345 \mat ...

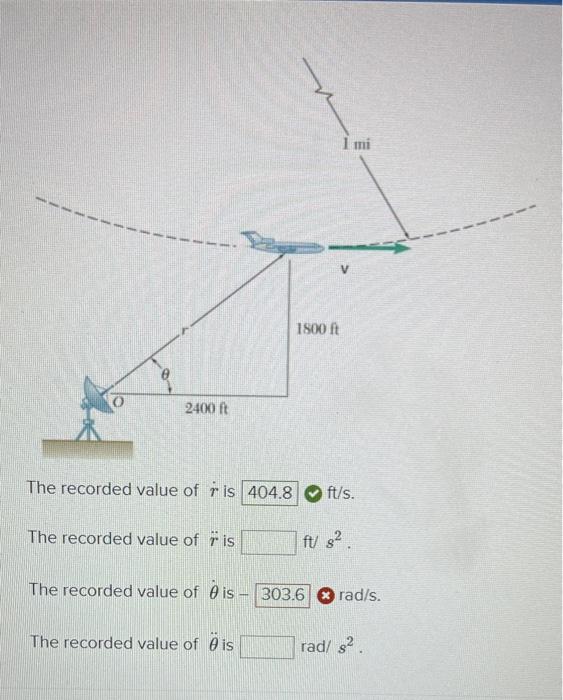
At the bottom of a loop in the vertical plane, an airplane has a horizontal velocity of \( 345 \mathrm{mi} / \mathrm{h} \) and is speeding up at a rate of \( 10 \mathrm{ft} / \mathrm{s} \) ? The radius of curvature of the loop is \( 1 \mathrm{mi} \). The plane is being tracked by radar at 0 . What are the recorded values of \( \dot{r}, \vec{r}, \dot{\theta} \), and \( \ddot{\theta} \) for this instant? The recorded value of \( \mathrm{ris} \) The recorded value of \( \dot{r} \) is \( \mathrm{ft} / \mathrm{s} \). The recorded value of \( \ddot{r} \) is \( \mathrm{ft} \mathrm{s}^{2} \). The recorded value of \( \dot{\theta} \) is - \( \boldsymbol{r a d} / \mathrm{s} \). The recorded value of \( \ddot{\theta} \) is \( \mathrm{rad} / \mathrm{s}^{2} \).