(Solved): As shown below, a motor runs at 1,750 rpm, and this motor drives a blower using a belt drive. The b ...

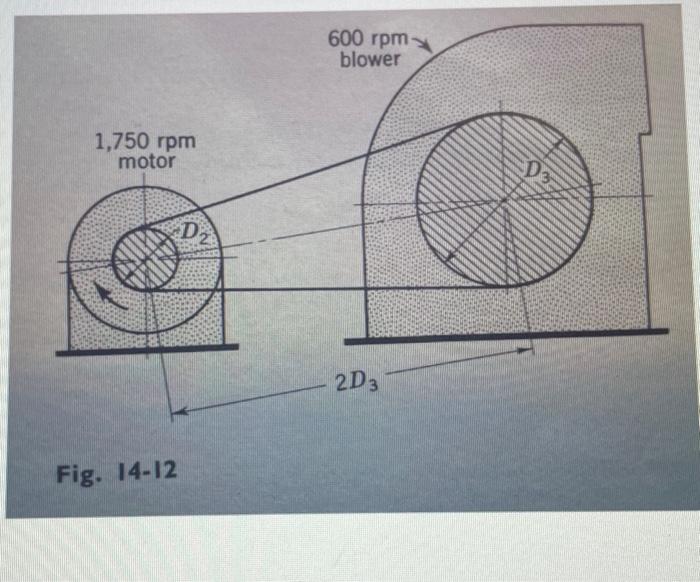
As shown below, a motor runs at 1,750 rpm, and this motor drives a blower using a belt drive. The blower operates at $600\mathrm{rpm}$. The pulley attached to the motor shaft is pulley 2 , and the pulley attached to the blower shaft is pulley 3. The diameter of the pulley attached to the motor shaft is $D_2$, and the diameter of the pulley attached to the blower shaft is $D_3$. The center distance between the two shafts is twice the diameter of pulley 3. Design the belt drive system by determining the following: a) (5 points) The required diameters of both pulleys. b) (5 points) The length of the belt to be used in the drive system. c) (5 points) The angles of wrap for pulley 2 and pulley 3. d) (5 points) The minimum initial tension, $F_0$, required so that neither pulley will slip against the belt (determinatiohof $F_o$ will require finding the tight side and slack side belt tensions, $F_1$ and $F_2$ respectively). The belt manufacturer specifies that the proper operating linear velocity of the belt is $4000\mathrm{fpm}$ (feet per minute). Assume belt stretch is negligible. If the belt tension in part c) is specified correctly, then no belt slip may be assumed. The belt is leather, and the pulleys are cast iron. The coefficient of friction between pulley 3 and the belt is ${?}_3=0.40$. However, pulley 2 is wrapped, on its outside diameter, with a nonmetallic material to increase beit to pulley friction. Therefore, the coefficient of friction between pulley 2 and the belt is ${?}_2=0.50$. The value of $F_c$ is $100\mathrm{lbs}$, and the value of $F_2$ is $210\mathrm{lbs}$. Fig. 14-12