(Solved): answer those 5 questions please The table of values represents a polynomial function. The function a ...

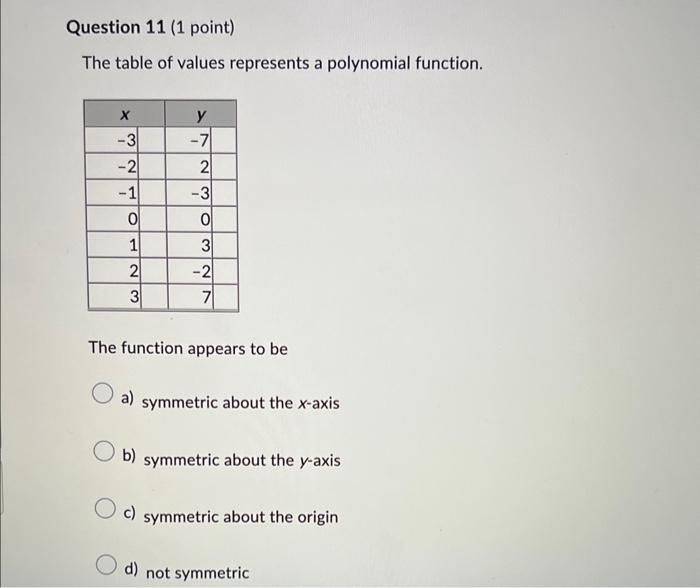
The table of values represents a polynomial function. The function appears to be a) symmetric about the \( x \)-axis b) symmetric about the \( y \)-axis c) symmetric about the origin d) not symmetric Find the quadratic factor, \( x^{2}+b x+c \), of a polynomial function that would produce the zeros \( \pm 3 \sqrt{5} \). 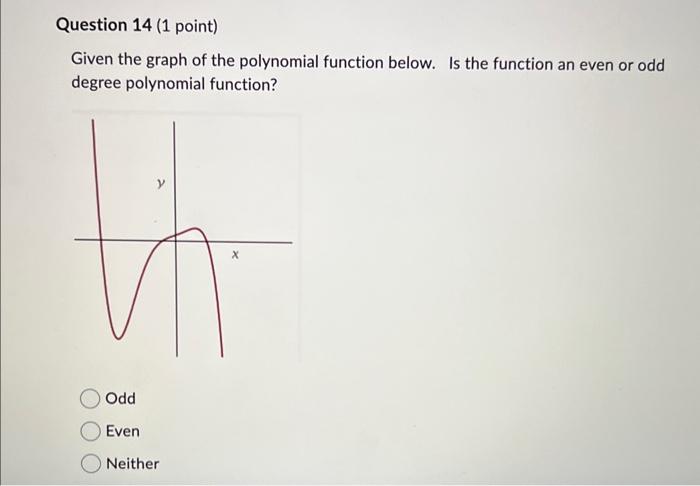\[ x^{2}+2 x-45 \] \[ x^{2}-45 \] \[ x^{2}+45 \] \[ x^{2}-2 x-45 \] The function \( y=(x-1)(x-2)(x-3) \) is negative on the interval(s) a) \( x \hat{\imath}(-\not, 1) \) and \( x \hat{\imath}(2,3) \) b) \( x \hat{\imath}(1,2) \) c) \( x \hat{\imath}(1,2) \) and \( x \hat{\imath}(3,7) \) d) \( x \hat{\imath}(2,3) \) Given the graph of the polynomial function below. Is the function an even or odd degree polynomial function? Odd Even Neither Given the function \( f(x)=\left(-\left(3((-(2 x))-6)^{3}\right)\right)-3 \), if we were to write it in the form \( f(x)=a(x-h)^{n}+k \), determine the value of each parameter. \( \mathrm{a}, \mathrm{h}, \mathrm{n} \) and \( \mathrm{k} \) in order. \[ \begin{array}{l} 24,-3,-3,-3 \\ 24,-3,3,-3 \\ 24,3,3,-3 \\ -24,-3,3,-3 \end{array} \]